Trees

• A tree is an abstract model of a heirarchical structure
• A tree consists of nodes with a parent-child relationship
  • A parent has one or more children
  • Each child has only one parent
• The root is the top node in the tree, the only node without a parent
• An internal node has at least one child
• An external node (or leaf) is a mode with no children
• Nodes have ancestors (ie, the parent node of a parent)
• The depth of a node is its number of ancestors
• The height of a tree is its maximum depth

Tree ADT

Tree ADTs are defined using a similar concept to positional lists, as they don't have a natural ordering/indexing in the same way arrays do.

public interface Tree<E>{
    int size();
    boolean isEmpty();
    Node<E> root(); //returns root node
    Node<E> parent(Node<E> n); //returns parent of Node n
    Iterable<Node<E>> children(Node<E> n); //collection of all the children of Node n
    int numChildren(Node<E> n);
    Iterator<E> iterator(); //an iterator over the trees elements
    Iterator<Node<E>> nodes(); //collection of all the nodes
    boolean isInternal(Node<E> n); //does the node have at least one child
    boolean isExternal(Node<E> n); //does the node have no children
    boolean isRoot(Node<E> n); //is the node the root

}

Tree Traversal

Trees can be traversed in 3 different orders. As trees are recursive data structures, all 3 traversals are defined recursively. The tree below is used as an example in all 3 cases.

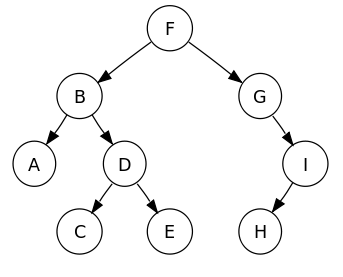
Pre-order

• Visit the root
• Pre order traverse the left subtree
• Pre order traverse the right subtree

Pre-order traversal of the tree gives: F B A D C E G I H

In-order

• In order traverse the left subtree
• Visit the root
• In order traverse the right subtree

In-order traversal of the tree gives: A B C D E F G H I

Post-order

• Post order traverse the left subtree
• Post order traverse the right subtree
• Visit the root

Post-order traversal of the tree gives: A C E D B H I G F

Binary Trees

A binary tree is a special case of a tree:

• Each node has at most two children (either 0, 1 or 2)
• The children of the node are an ordered pair (the left node is less than the right node)

A binary tree will always fulfil the following properties:

• $e=i+1$
• $n=2e-1$
• $h\le i$
• $h\le (n-1)/2$
• $e\le 2^h$
• $h\ge {\log }_{2}e$
• $h\ge {\log }_2(n+1)-1$

Where:

• $n$ is the number of nodes in the tree
• $e$ is the number of external nodes
• $i$ is the number of internal nodes
• $h$ is the height/max depth of the tree

Binary Tree ADT

The binary tree ADT is an extension of the normal tree ADT with extra accessor methods.

public interface BinaryTree<E> extends Tree<E>{
    Node<E> left(Node<E> n); //returns the left child of n
    Node<E> right(Node<E> n); //returns the right child of n
    Node<E> sibling(Node<E> n); //returns the sibling of n
}

Arithmetic Expression Trees

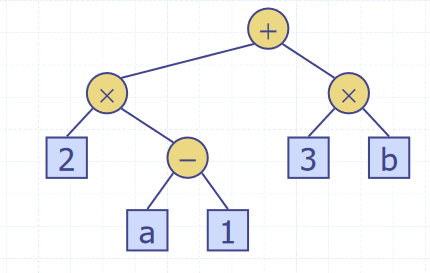
Binary trees can be used to represent arithmetic expressions, with internal nodes as operators and external nodes as operands. The tree below shows the expression $(2\times (a-1))+(3\times b)$. Traversing the tree in-order will can be used to print the expression infix, and post-order evaluating each node with it's children as the operand will return the value of the expression.

Implementations

• Binary trees can be represented in a linked structure, similar to a linked list
• Node objects are positions in a tree, the same as positions in a positional list
• Each node is represented by an object that stores
  • The element
  • A pointer to the parent node
  • A pointer to the left child node
  • A pointer to the right child node
• Alternatively, the tree can be stored in an array A
• A[root] is 0
• If p is the left child of q, A[p] = 2 * A[q] + 1
• If p is the right child of q, A[p] = 2 * A[q] + 2
• In the worst, case the array will have size $2^n-1$

Binary Search Trees

• Binary trees can be used to implement a sorted map
• Items are stored in order by their keys
• For a node $p$ with key $K_p$, every key in the left subtree is less than $K_p$, and every node in the right subtree is greater than $K_p$
• This allows for support of nearest-neighbour queries, so can fetch the key above or below another key
• Binary search can perform nearest neighbour queries on an ordered map to find a key in $O(\log n)$ time
• A search table is an ordered map implemented using a sorted sequence
  • Searches take $O(\log n)time$
  • Insertion and removal take $O(n)$ time
  • Only effective for maps of small size

Methods

Binary trees are recursively defined, so all the methods operating on them are easily defined recursively also.

• Search
• To search for a key $K$
  • Compare it with the key at $K_{root}$
  • If $K_{root}=K$, the value has been found
  • If $K_{root}<K$, search the right subtree
  • If $K_{root}>K$, search the left subtree
• Insertion
  • Search for the key being inserted $K$
  • Insert $K$ at the leaf reached by the search
• Deletion
  • Find the internal node that is follows the key being inserted in an in order traversal (the in order successor)
  • Copy key into the in order successor node
  • Remove the node copied out of

Performance

• Consider a binary search tree with $n$ items and height $h$
• The space used is $O(n)$
• The methods get, put, remove take $O(h)$ time
  • The height h is $O(\log n)$ in the best case, when the tree is perfectly balanced
  • In the worst case, when the tree is basically just a linked list, this decays to $O(n)$

AVL Trees

• AVL trees are balanced binary trees
  • For every internal node $v$ of the tree, the heights of the subtrees of $v$ can differ by at most 1
• The height of an AVL tree storing $n$ keys is $O(\log n)$
• Balance is maintained by rotating nodes every time a new one is inserted/removed

Performance

• The runtime of a single rotation is $O(1)$
• The tree is assured to always have $h=\log n$, so the runtime of all methods is $O(\log n)$
• This makes AVL trees an efficient implementation of binary trees, as their performance does not decay as the tree becomes unbalanced