Mesh Analysis

Achieves a similar thing to nodal analysis, using Kirchhoff's voltage law, and meshes instead of nodes.

Kirchhoff's Voltage Law

The sum of voltages around a closed loop always equals zero

$- V_{1} + V_{2} - V_{3} - V_{4} = 0$

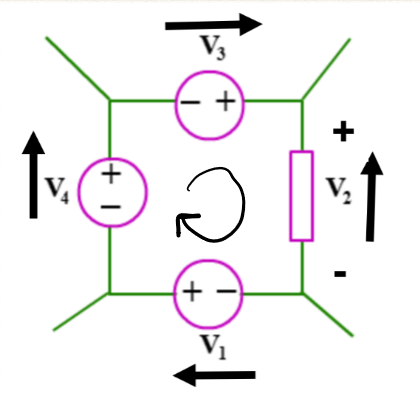
Sign convention

If voltage rise and current in a voltage source are in the same direction, the voltage is denoted as negative
If voltage rise and current are in opposite direction, voltage is positive
In a resistor, current opposes voltage rise

Steps

Identify meshes (loops) (always clockwise) and assign currents $I_{1}, I_{2},$ etc to those loops
Apply KVL to each mesh to generate system of equations
Solve equations

Where there are elements that are part of multiple meshes, subtract the currents of the other meshes from the mesh currently being considered to consider the total current through that circuit element.

Example

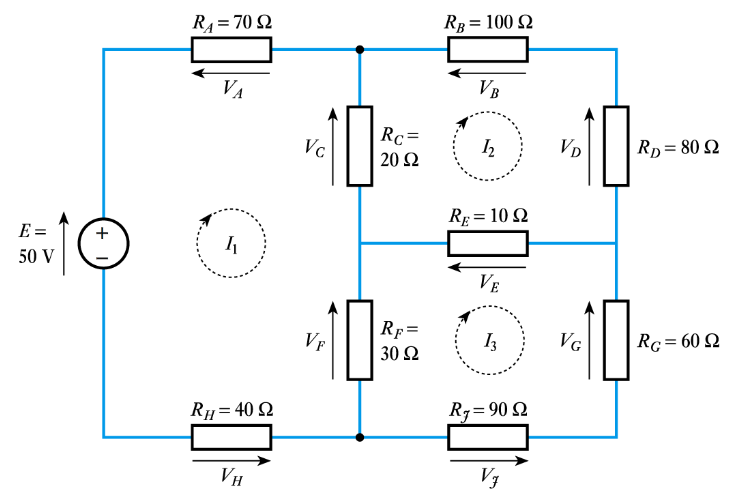
There are three meshes in this circuit, labelled $I_{1}$ , $I_{2}$ , $I_{3}$ .

For $I_{1}$ : $- 50 + 70 I_{1} + 20 (I_{1} - I_{2}) + 30 (I_{1} - I_{3}) + 40 I_{1} = 0$

For $I_{2}$ : $20 (I_{2} - I_{1}) + 100 I_{2} + 80 I_{2} + 10 (I_{2} - I_{3}) = 0$

For $I_{3}$ : $30 (I_{3} - I_{1}) + 10 (I_{3} - I_{2}) + 60 I_{3} + 90 I_{3} = 0$

This forms a system of equations:

$160 I_{1} - 20 I_{2} - 30 I_{3} = 50 - 20 I_{1} + 210 I_{2} - 10 I_{3} = 0 - 30 I_{1} - 10 I_{2} + 190 I_{3} = 0$

Solving yields $I_{1} = 325 m A$ , $I_{2} = 34 m A$ , and $I_{3} = 53 m A$ .

Impedance Matrices

Similar to how systems of equations from nodal analysis form admittance matrices, mesh analysis forms impedance matrices which describe the circuit being analysed. The matrix equation takes the form $Z \cdot I = V$ . As an example, the matrix equation for the system above is:

$160 - 20 - 30 - 20 210 - 10 - 30 - 10 190 I_{1} I_{2} I_{3} = 5000$

Therefore, the impedance matrix for the system is:

$Z = 160 - 20 - 30 - 20 210 - 10 - 30 - 10 190$

Another Example

Determine the currents in the circuit shown below:

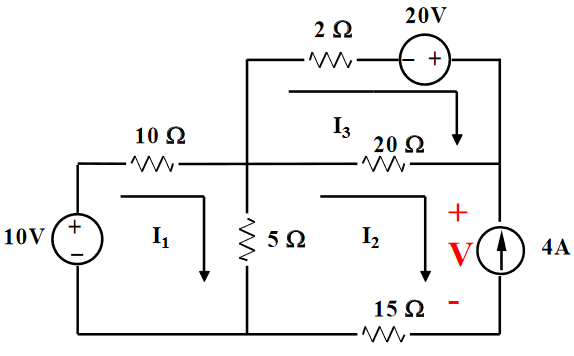
Loop 1: $- 10 + 10 I_{1} + 5 (I_{1} - I_{2}) = 0$

Loop 2: $5 (I_{2} - I_{1}) + 20 (I_{2} - I_{3}) + V + 15 I_{2} = 0$

Where there is a current source, a voltage $V$ is assumed accross it.

Loop 3: $2 I_{3} - 20 + 20 (I_{3} - I_{2}) = 0$

There are now 3 equations with 4 unknowns. However, it can be seen from the diagram that $I_{2} = - 4 A$ (the direction of the current source opposes our clockwise current), so the system can be solved as follows:

$I_{2} = - 4 A$ $I_{1} = \frac{10 + 5 I _{2}}{15} = - 0.67 A$ $I_{3} = \frac{20 + 20 I _{2}}{22} = - 2.73 A$

Example with dependant sources

Calculate the power dissapated in the 4 $Ω$ resistor and the power delivered/absorbed by the current dependant voltage source.

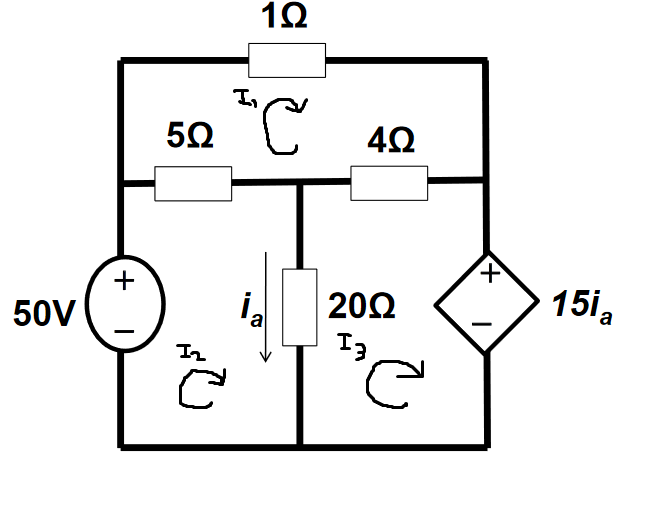
KVL round $I_{1}$ :

$I_{1} + 4 (I_{1} - I_{3}) + 5 (I_{1} - I_{2}) = 0$

KVL round $I_{2}$ :

$5 (I_{2} - I_{1}) + 20 (I_{2} - I_{3}) - 50 = 0$

KVL round $I_{3}$ :

$15 I_{a} + 20 (I_{3} - I_{2}) + 4 (I_{3} - I_{1}) = 0$

$I_{a} = I_{2} - I_{3}$ , so this can be substituted into equation 3 to obtain a fourth equation:

$15 (I_{2} - I_{3}) + 20 (I_{3} - I_{2}) + 4 (I_{3} - I_{1}) = 0$

The system of equations then solves:

$10 - 5 - 4 - 5 25 - 5 - 4 - 20 9 I_{1} I_{2} I_{3} = 0500 ⟹ I_{1} I_{2} I_{3} = 26 29.6 28$

The power dissapated in the 4 $Ω$ resistor: $P = I^{2} R = 2^{2} \times 4 = 16 W$

The power delivered/absorbed by the dependant voltage source: $P = I V = 15 I_{a} \times I_{2} = 15 (29.6 - 28) \times 28 = 672 W (ab sor bin g)$ The source is absorbing power as the current $I_{2}$ opposes the direction of voltage rise in the source.

Computer Systems Engineering Notes