Functions, Conics & Asymptotes

Domain & Range

• The domain of a function is the set of all valid/possible input values
  • The x axis
• The range of a function is the set of all possible output values
  • The y axis

Odd & Even Functions

$$f(x)=f(-x)\Rightarrow \text{f is even}$$ $$f(-x)=-f(x)\Rightarrow \text{f is odd}$$ $$f(x)=-f(-x)\Rightarrow \text{f is odd}$$

Conics

Equation of a circle with radius $r$ and centre $(x_0,y_0)$ $$(x-x_0{)}^2+(y-y_0{)}^2=r^2$$

Equation of an ellipse with centre $(x_0,y_0)$, major axis length $2a$ and minor axis length $2b$: $$\frac{(x-x_0{)}^2}{a^2}+\frac{(y-y_0{)}^2}{b^2}=1$$

Equation of a Hyperbola with vertex $(x_0,y_0)$:

$$\pm \frac{(x-x_0{)}^2}{a^2}\mp \frac{(y-y_0{)}^2}{b^2}=1$$ The asymptotes of this hyperbola are at: $$(y-y_0)=\pm \frac{b}{a}(x-x_0)$$

Asymptotes

There are 3 kinds of asymptotes:

• Vertical
• Horizontal
• Oblique (have slope)

For a function $y=\frac{P(x)}{Q(x)}$:

• Vertical asymptotes lie where $Q(x)=0$ and $P(X)\ne 0$
• Horizontal asymptotes
  • If the degree of the denominator is bigger than the degree of the numerator, the horizontal asymptote is the x-axis
  • If the degree of the numerator is bigger than the degree of the denominator, there is no horizontal asymptote.
  • If the degrees of the numerator and denominator are the same, the horizontal asymptote equals the leading coefficient of the numerator divided by the leading coefficient of the denominator
• Oblique asymptotes
  • A rational function will approach an oblique asymptote if the degree of the numerator is one order higher than the order of the denominator
  • To find
    • Divide $P(x)$ by $Q(x)$
    • Take the limit as $x\to \infty$

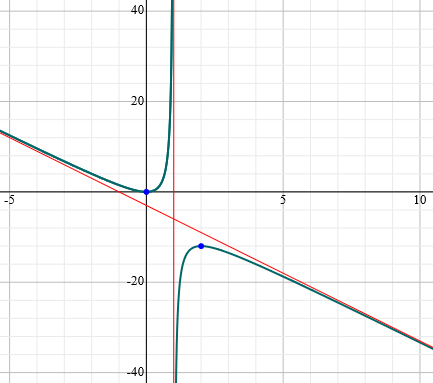
Example: find the asymptotes of $y=\frac{-3x^2+2}{x-1}$:

• Vertical asymptotes:
  • Where the denominator is 0

$$x-1=0\Rightarrow x=1$$

• Horizontal asymptotes:
  • There are none, as degree of the numerator is bigger than the degree of the denominator
• Oblique asymptotes:
  • Divide the top by the bottom using polynomial long division
  • Find the limit

$$y=\frac{-3x^2}{x-1}=-3x-3+\frac{-1}{x-1}$$

As $x\to \infty$, $y\to -3x-3$, giving $y=-3x-3$ as an asymptote.