Vectors

Vector Equation of a Straight Line

The vector $\mathbf{r}$ is the vector of any point along the line.

$$\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}$$

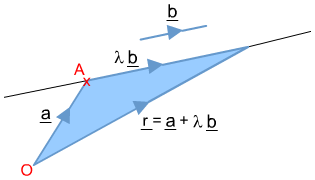
$\mathbf{a}$ is any point on the line, and \bm{b} is the direction of the line. $\lambda$ is a parameter that represents the position of $\mathbf{r}$ relative to $\mathbf{a}$ along the line. The carteian form of this can be derived: $$x=a_1+\lambda b_1$$ $$y=a_2+\lambda b_2$$ $$z=a_3+\lambda b_3$$

Equating about lambda: $$\frac{x-a_1}{b_1}=\frac{y-a_2}{b_2}=\frac{z-a_3}{b_3}$$

Scalar/Dot Product

The dot product of two vectors: $$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos \theta =\sum a_n{b}_n$$

• If $\mathbf{a}\cdot \mathbf{b}=0$, then $\theta =90$ and $\cos \theta =0$
  • The two vectors are perpendicular
• $\mathbf{a}\cdot \mathbf{a}=|\mathbf{a}{|}^2$

The angle between two vectors can be calculated using the dot product $$\cos \theta =\frac{\mathbf{a}\cdot \mathbf{b}}{|\mathbf{b}||\mathbf{a}|}$$

Projections

The projection of vector $\mathbf{a}$ in the direction of $\mathbf{b}$ is given by the scalar product:

$$\frac{\mathbf{b}}{|\mathbf{b}|}\cdot \mathbf{a}=\hat{\mathbf{b}}\cdot \mathbf{a}$$

This gives a vector in the direction of $\mathbf{b}$ with the magnitude of $\mathbf{a}$.

Equation of a Plane

The vector equation of a plane is given by $$\mathbf{r}\cdot \mathbf{n}=\mathbf{a}\cdot \mathbf{n}$$

Where $\mathbf{n}$ is the normal to the plane, and $\mathbf{a}$ is any point in the plane. This expands to the cartesian form:

$$n_{1}x+n_{2}y+n_{3}z=\mathbf{a}\cdot \mathbf{n}$$

Angle Between Planes

The angle between two planes is given by the angle between their normals. $$\cos \theta =\frac{{\mathbf{n}}_1\cdot {\mathbf{n}}_2}{|{\mathbf{n}}_1||{\mathbf{n}}_2|}$$

Intersection of 2 Planes

Two planes will only intersect if their normal vectors intersect.

• First, check the two normals are non parallel
  • ${\mathbf{n}}_1\cdot {\mathbf{n}}_2\ne 0$
• Equate all 3 variables about either a parameter $\lambda$ or one of $x$, $y$, or $z$ to get an equation for the line along which the planes intersect in cartesian form

Example

Find the intersection of the planes $3x+y-4z=4$ (1) and $-x+y=2$ (2).

(1) - (2): $$4x-6z=2\Rightarrow z=\frac{2x-1}{3}$$

(1) + 3(2): $$4y+2z=10\Rightarrow z=\frac{2y-5}{-1}$$

Equating the two with z:

$$\frac{2x-1}{3}=\frac{2y-5}{-1}=z$$

Using Cross Product

For two normals to planes ${\mathbf{n}}_1$ and ${\mathbf{n}}_2$, the vector $\mathbf{b}={\mathbf{n}}_1\times {\mathbf{n}}_2$ will lie in both planes. The line

$$\mathbf{r}=\mathbf{a}+\lambda ({\mathbf{n}}_1\times {\mathbf{n}}_2)$$

lies in both planes.

Distance from Point to Plane

The shortest distance from the point $(x_0,y_0,z_0)$ to the plane $Ax+By+Cz+D=0$ is given by:

$$\frac{|A{x}_0+B{y}_0+C{z}_0+D|}{\sqrt{A^2+B^2+C^2}}$$

Vector/Cross Product

The cross product of two vectors produces another vector, and is defined as follows

$$\mathbf{a}\times \mathbf{b}=|\mathbf{a}||\mathbf{b}|\sin \theta \hat{\mathbf{n}}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_x& a_y& a_z\\ b_x& b_y& b_z\end{array}\right|$$

$\theta$ is the angle between the two vectors, and $\hat{\mathbf{n}}$ is a unit vector perpendicular to both $\mathbf{a}$ and $\mathbf{b}$. The right-hand rule convention dictates that $\hat{\mathbf{n}}$ should always point up (ie, if $\mathbf{a}$ and $\mathbf{b}$ are your fingers, then $\hat{\mathbf{n}}$ is your thumb). The cross product is not commutative, as $\mathbf{a}\times \mathbf{b}$ = $-(\mathbf{b}\times \mathbf{a})$.

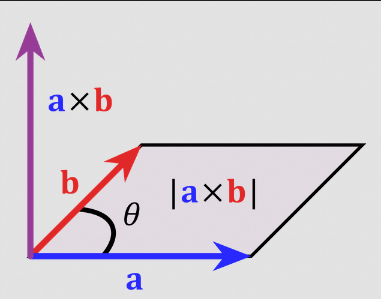
• The magnitude of the cross product $|\mathbf{a}\times \mathbf{b}|$ is equal to the area of the parallelogram formed by the two vectors.
• Can be used to find a normal given 2 vectors/2 points in a plane

Angular Velocity

A spheroid rotates with angular velocity $\mathbf{\omega }$. A point $\mathbf{A}$ on the spheroid has velocity $\mathbf{v}=\mathbf{\omega }\times \mathbf{A}$