Binomial Theorem & Taylor Series

Binomial Theorem

Taking powers of binomial expressions yields binomial expressions, the coefficients of which form pascals triangle:

$$(a+b{)}^0=1$$

$$(a+b{)}^1=a+b$$

$$(a+b{)}^2=a^2+2ab+b^2$$

$$(a+b{)}^3=a^3+3a^{2}b+3a{b}^2+b^3$$

This can be generalised to:

$$(a+b{)}^n=a^n+n{a}^{n-1}b+\frac{n(n-1)}{2!}{a}^{n-2}{b}^2+...+b^n$$

For the particular case where $a=1$ and $b=x$,we have:

$$(1+x{)}^n=1+nx+\frac{n(n-1)}{2!}{x}^2+\frac{n(n-1)(n-2)}{3!}{x}^3+...+x^n$$

When $n$ is not a positive integer and $-1<x<1$:

$$(1+x{)}^n=1+nx+\frac{n(n-1)}{2}{x}^2+...+\frac{n(n-1)...(n-r-1)}{r!}{x}^r...$$

Note that this is now an infinite series which converges. Can be used to approximate functions by ignoring higher order terms.

Sequences

A sequence is any arrangement of numbers, functions, terms, etc, in a specific order.

• May be finite or infinite
• The $k^{th}$ term of the sequence $Z$ is denoted $Z[k]$

A sequence of functions, $Z$:

$$Z[1]=(1+\frac{x}{2})Z[2]=(1+\frac{x}{3}{)}^{2}Z[3]=(1+\frac{x}{4}{)}^3$$

$$Z[k]=(1+\frac{x}{k+1}{)}^{k}k=1,2,3,\mathrm{4...}$$

Series

A series is obtained by summing a sequence

$$\sum _{k=0}^{\infty }(\frac{1}{4}{)}^k=1+\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+...$$

Arithmetic sequences/series have a common difference, $d$, between terms

$$a,a+d,a+2d,...$$

$$Z[k]=a+(k-1)d$$

$$S_n=\frac{n}{2}(2a+(n-1)d)$$

Geometric series are obtained by multiplying the previous term by a fixed number, the common ratio

$$a,ar,a{r}^2,...$$

$$Z[k]=a{r}^{(k-1)}$$

$$S_n=\frac{a(1-r^n)}{1-r}$$

Limits

It is important to know if a sequence converges to a value as $k\to \infty$, or diverges to $\pm \infty$ as $k\to \infty$. Consider:

$$1,\frac{1}{2},\frac{1}{3},\frac{1}{4},...,\frac{1}{k}$$

$$\underset{k\to \infty }{\lim }\frac{1}{k}=0$$

A sequence converges if it has a limit. If not, it diverges

Converge of Infinite Series

Manipulating the sequence can make it easier to see if the sequence converges or diverges. For example:

$$x[k]=\frac{2k^2+3k-1}{7k^2+4k+2},k=1,2,3,...$$

Divide by the highest power of k:

$$\frac{2+\frac{3}{k}-\frac{1}{k^2}}{7+\frac{4}{k}+\frac{2}{k^2}}$$

Since $\frac{1}{k}$ and $\frac{1}{k^2}$ both tend to 0 as ${\lim }_{k\to \infty }$, the sum is convergent.

Another example, consider the series

$$\sum _{k=1}^{\infty }\frac{1}{\sqrt{k}}=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{n}}+...$$

Clearly, ${\lim }_{k\to \infty }\frac{1}{\sqrt{k}}=0$, however the partial sum $S_n$ (the sum of terms up to $n$) has $n$ terms, the smallest being $\frac{1}{\sqrt{n}}$. Thus:

$$S_n\ge n(\frac{1}{\sqrt{n}})=\sqrt{n},\Rightarrow \underset{n\to \infty }{\lim }{S}_n\to \infty$$

The series is divergent, as can be seen from the limit of partial sums. In order to see whether an infinite series converges to a limit, $S$, (a finite sum for infinite number of terms) we look at the sequence of partial sums, $S_n$, up to $n$ terms. Another example:

$$\sum _{k=1}^{\infty }(\frac{1}{k}-\frac{1}{k+1})=\underset{k\to \infty }{\lim }\left[\left(\frac{1}{1}-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+...+\left(\frac{1}{k}-\frac{1}{k+1}\right)\right]$$

Sequence of partial sums:

$$S_1=\left(\frac{1}{1}-\frac{1}{2}\right)=\frac{1}{2}$$

$$S_2=\left(\frac{1}{1}-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)=\frac{2}{3}$$

$$S_2=\left(\frac{1}{1}-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)=\frac{3}{4}$$

$$\underset{n\to \infty }{\lim }{S}_n=\underset{n\to \infty }{\lim }\left[1-\frac{1}{n+1}\right]=1-0=1$$

The sequence of partial sums shows that the series converges.

• Infinite arithmetic series are always divergent.
• Infinite geometric series are convergent iff $|r|<1$
  • Sum is $\frac{a}{1-r}$

Tests for Convergence

Comparison Test

A series of positive terms is convergent if the value of each of its terms is less than or equal to the corresponding terms of another series of positive terms that is convergent.

A series of positive terms is divergent if the value of each of its terms is greater than or equal to the corresponding terms of another series of positive terms that is divergent

Ratio Test

The series of positive terms

$$\sum _{k=1}^{\infty }{a}_k=a_1+a_2+...+a_k+...$$

is convergent if:

$$\underset{k\to \infty }{\lim }\frac{a_{k+1}}{a_k}<1$$

and divergent if:

$$\underset{k\to \infty }{\lim }\frac{a_{k+1}}{a_k}>1$$

Example

Testing the following sequence $S$ for convergence:

$$S=\sum _{k=1}^{\infty }\frac{1}{k{3}^{k-1}}=1+\frac{1}{2\times 3}+\frac{1}{3\times 3^2}+...$$

Compare it with a sequence less than it that is known to be convergent:

$$1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{k-1}}+...$$

$$1=1$$

$$\frac{1}{2\times 3}<\frac{1}{3}$$

$$\frac{1}{3\times 3^2}<\frac{1}{3^2}$$

$$\frac{1}{3^{k-1}}<\frac{1}{3^{k-1}}$$

Thus $S$ is convergent.

Taylor & Maclaurin Series

Taylor and Maclaurin series provide polynomial approximations to any function. Suppose that a function $f(x)$ is infinitely differentiable, and its derivatives known at a particular point, $x^{\ast }=a$. This function can then be expressed as an infinite polynomial series.

$$f(x)=\sum _{n=0}^{\infty }{c}_n(x-a{)}^n=c_0+c_1(x-a)+c_2(x-a{)}^2+c_3(x-a{)}^3+...$$

This series can be repeatedly differentiated to obtain values for all the constants:

$$c_0=a{c}_1=f^{\prime }(a)c_2=\frac{1}{2!}{f}^{(2)}(a)...c_n=\frac{1}{n!}{f}^{(n)}(a)$$

Therefore the Taylor series expansion of $f(x)$ about the point x^{*} = a is:

$$f(x)=\sum _{n=0}^{\infty }\frac{1}{n!}{f}^{(n)}(a)(x-a{)}^n=f(a)+f^{\prime }(a)(x-a)+\frac{1}{2!}{f}^{(2)}(a)(x-a{)}^2+...+\frac{1}{n!}{f}^{(n)}(a)(x-a{)}^n$$

Alternatively expressed as

$$f(a+h)=f(a)+h{f}^{\prime }(a)+\frac{h^2}{2!}{f}^{(2)}(a)+...+\frac{h^n}{n!}{f}^{(n)}(a)$$

Maclaurin Series

If expanding about the point $a=0$, then the Taylor series becomes the Maclaurin series:

$$f(x)=\sum _{n=0}^{\infty }\frac{1}{n!}{f}^{(n)}(0)x^n=f(0)+f^{\prime }(0)x+\frac{1}{2!}{f}^{(2)}(0)x^2+...+\frac{1}{n!}{f}^{(n)}(0)x^n$$

Example

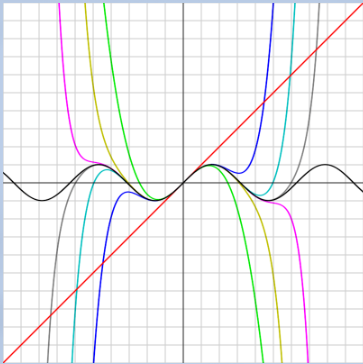
Finding Maclaurin series for $\sin (x)$:

$$f(0)=\sin (0)=0$$

$$f^{\prime }(0)=\cos (0)=1$$

$$f^{\prime \prime }(0)=-\sin (0)=0$$

$$f^{\prime \prime \prime }(0)=-\cos (0)=-1$$

$$f(x)=f(0)+f^{\prime }(0)x+\frac{1}{2!}{f}^{(2)}(0)x^2+\frac{1}{3!}{f}^{(2)}(0)x^3+...$$

$$f(x)=0+1x+\frac{1}{2!}0x^2-\frac{1}{3!}{f}^{(2)}(0)x^3+...$$

$$f(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-...$$

$$f(x)=\sum _{n=0}^{\infty }\frac{(-1{)}^k}{(2k+1)!}{x}^{2k+1}=\sin (x)$$

The image below shows the polynomial maclaurin approximations to $\sin (x)$ for increasing $n$. You can see how accuracy improves as $n\to \infty$