Graphs

A graph is a collection of edges and vertices, a pair $(V, E)$ , where

$V$ is a set of nodes, called vertices
$E$ is a collection of pairs of vertices, called edges
Vertices and edges are positions and store elements

Examples of graphs include routes between locations, users of a social network and their friendships, and the internet.

There are a number of different types of edge in a graph, depending upon what the edge represents:

Directed edge
- Ordered pair of vertices $(u, v)$
- First vertex $u$ is the origin
- Second vertex $v$ is the destination
- For example, a journey between two points
Undirected edge
- Unordered pair of vertices $(u, v)$
In a directed graph, all edges are directed
In an undirected graph, all edged are undirected

Graph Terminology

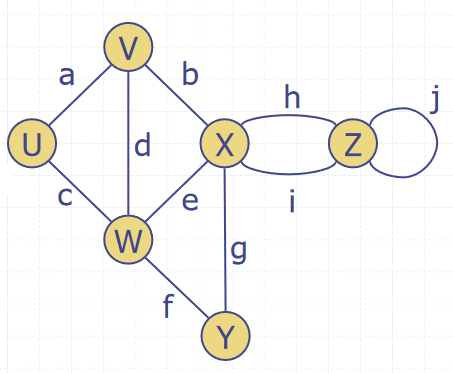
Adjacent vertices
- Two vertices $U$ and $V$ are adjacent (ie connected by an edge)
Edges incident on a vertex
- The edges connect to a vertex
- $a$ , $d$ , and $b$ are incident on $V$
End vertices or endpoints of an edge
- The vertices connected to an edge
- $U$ and $V$ are endpoints of $a$
The degree of a vertex
- The number of edges connected to it
- $X$ has degree 5
Parallel edges
- Edges that make the same connection
- $h$ and $i$ are parallel
Self-loop
- An edge that has the same vertex at both ends
- $j$ is a self-loop
Path
- A sequence of alternating vertices and edges
- Begins and ends with a vertex
- Each edge is preceded and followed by its endpoints
- $P_{1} = (V, b, X, h, Z)$ is a simple path
Cycle
- A circular sequence of alternating vertices and edges
  - A circular path
- A simple cycle is one where all edges and vertices are distinct
- A non-simple cycle contains an edge or vertex more than once
- A graph without cycles (acyclic) is a tree
Length
- The number of edges in a path
- The number of edges in a cycle

Graph Properties

Notation:

$n$ is the number of vertices
$m$ is the number of edges
$de g (v)$ is the degree of vertex $v$

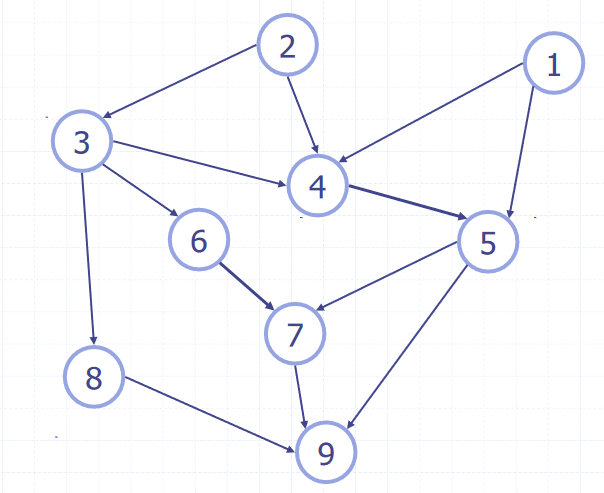
The sum of the degrees of the vertices of a graph is always an even number. Each edge is counted twice, as it connects to two vertices, so $\sum_{v} de g (v) = 2 m$ . For example, the graph shown has $n = 4$ and $m = 6$ . $de g (v) = 3 \Rightarrow \sum_{v} de g (v) = 2 m = 12$

In an undirected graph with no self loops and no multiple edges, $m \leq n \frac{n - 1}{2}$ . Each vertex has degree at most $(n - 1)$ and $\sum_{v} de g (v) = 2 m$ . For the graph shown, $m = 6 \leq n \frac{n - 1}{2} = 6$

The Graph ADT

A graph is a collection of vertices and edges, which are modelled as a combination of 3 data types: Vertex, Edge and Graph.

A Vertex is just a box object storing an element provided by the user
An Edge also stores an associated value which can be retrieved

public interface Graph{
    int numVertices();

    Collection vertices(); //returns all the graph's vertices

    int numEdges();

    Collection<Edge> edges(); //returns all the graph's edges

    Edge getEdge(u,v); //returns the edge between u and v, if on exists
    // for an undirected graph getEdge(u,v) == getEdge(v,u)

    Pair<Vertex, Vertex> endVertices(e); //returns the endpoint vertices of edge e

    Vertex oppsite(v,e); //returns the vertex adjacent to v along edge e

    int outDegree(v); //returns the number of edges going out of v

    int inDegree(v); //returns the number of edges coming into v
    //for an undirected graph, inDegree(v) == outDegree(v)

    Collection<Vertex> outgoingEdges(v); //returns all edges that point out of vertex v

    Collection<Vertex> incomingEdges(v); //returns all edges that point into vertex v
    //for an undirected graph, incomingEdges(v) == outgoingEdges(v)

    Vertex insertVertex(x); //creates and returns a new vertex storing element x

    Edge insertEdge(u,v,x); //creates and returns a new edge from vertices u to v, storing element x in the edge

    void removeVertex(v); //removes vertex v and all incident edges from the graph

    void removeEdge(e); //removes edge e from the graph
}

Representations

There are many different ways to represent a graph in memory.

Edge List

An edge list is just a list of edges, where each edge knows which two vertices it points to.

The Edge object stores
- It's element
- It's origin Vertex
- It's destination Vertex
The edge list stores a sequence of Edge objects

Adjacency List

In an adjacency list, each vertex stores an array of the vertices adjacent to it.

The Vertex object stores
- It's element
- A collection/array of all it's incident edges
The adjacency list stores all Vertex Objects

Adjacency Matrix

An adjacency matrix is an $n \times n$ matrix, where $n$ is the number of vertices in the graph. It acts as a lookup table, where each cell corresponds to an edge between two vertices.

If there is an edge between two vertices $u$ and $v$ , the matrix cell $(u, v)$ will contain the edge.
Undirected graphs are symmetrical along the leading diagonal

Subgraphs

A subgraph $S$ of a graph $G$ is a graph such that:
- The vertices of $S$ are a subset of the vertices of $G$
- The edges of $S$ are a subset of the edges of $G$
A spanning subgraph of $G$ is a subgraph that contains all the vertices of $G$
A graph is connected if there is a path between every pair of vertices
A tree is an undirected graph $T$ such that
- $T$ is connected
- $T$ has no cycles
A forest is an undirected graph without cycles
The connected components of a forest are trees

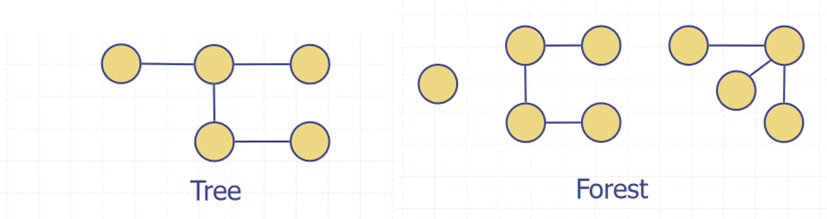
A spanning tree of a connected graph is a spanning subgraph that has all vertices covered with a minimum possible number of edges
- A spanning tree is not unique unless the graph is a tree
  - Multiple spanning trees exist
- Spanning trees have applications in the design of communication networks
- A spanning forest of a graph is a spanning subgraph that is a forest

Depth First Search

DFS is a general technique for traversing a graph. A DFS traversal of a graph $G$ will:

Visit all vertices and edges of $G$
Determine whether $G$ is connected
Compute the spanning components of $G$
Compute the spanning forest of $G$

DFS on a graph with $n$ vertices and $m$ edges takes $O (n + m)$ time. The algorithm is:

For a graph $G$ and a vertex $u$ of $G$
Mark vertex $u$ as visited
For each of $u$ 's outgoing edges $e = (u, v)$
- If $v$ has not been visited then
  - Record $e$ as the discovery edge for vertex $v$
  - Recursively call DFS with on $v$

DFS(G,V) visits all vertices and edges in the connected component of v, and the discovery edges labelled by DFS(G,V) form a spanning tree of the connected component of v.

DFS can also be extended to path finding, to find a path between two given vertices $u$ and $v$ . A stack is used to keep track of the path, and the final state of the stack is the path between the two vertices. As soon as the destination vertex $v$ is encountered, the contents of the stack is returned.

DFS can be used for cycle detection too. A stack is used to keep track of the path between the start vertex and the current vertex. As soon as a back edge $(v, w)$ (an edge we have already been down in the opposite direction) is encountered, we return the cycle as the portion of the stack from the top to the vertex $w$ .

To perform DFS on every connected component of a graph, we can loop over every vertex, doing a new DFS from each unvisited one. This will detect all vertices in graphs with multiple connected components.

Breadth First Search

BFS is another algorithm for graph traversal, similar to DFS. It also requires $O (n + m)$ time. The difference between the two is that BFS uses a stack while DFS uses a queue. The algorithm is as follows:

Mark all vertices and edges as unexplored
Create a new queue
Add the starting vertex $s$ to the queue
Mark $s$ as visited
While the queue is not empty
- Pop a vertex $v$ from the queue
- For all neighbouts $w$ of $v$
  - If $w$ is not visited
    - Push $w$ into the queue
    - Mark $w$ as visited

For a connected component $G_{s}$ of graph $G$ containing $s$ :

BFS visits all vertices and edges of $G_{s}$
The discovery edges labelled by BFS(G,s) form a spanning tree of $G_{s}$
The path of the spanning tree formed by the BFS is the shortest path between the two vertices

BFS can be specialised to solve the following problems in $O (n + m)$ time:

Compute the connected components of a graph
Compute a spanning forest of a graph
Find a simple cycle in G
Find the shortest path between two vertices
- DFS cannot do this, this property is unique to BFS

Directed Graphs

A digraph (short for directed graph) is a graph whose edges are all directed.

Each edge goes in only one direction
Edge $(a, b)$ goes from a to b but not from b to a
If the graph is simple and has $n$ vertices and $m$ edges, $m \leq n \frac{n - 1}{2}$
DFS and BFS can be specialised to traversing directed edges
- A directed DFS starting at a vertex $s$ determines the vertices reachable from $s$
- One vertex is reachable from another if there is a directed path to it

Strong Connectivity

A digraph is said to be strongly connected if each vertex can reach all other vertices. This property can be identified in $O (n + m)$ time with the following algorithm:

Pick a vertex $v$ in the graph $G$
Perform a DFS starting from $v$
- If theres a vertex not visited, return false
Let $G^{'}$ be $G$ with all the edge directions reversed
Perform a DFS starting from $v$ in $G^{'}$
- If theres a vertex not visited, return false
- Else, return True

Transitive Closure

Given a digraph $G$ , the transitive closure of $G$ is the digraph $G *$ such that:

$G *$ has the same vertices as $G$
If $G$ has a directed path from $u$ to $v$ , then G* also has a directed *edge* from $u$ to $v$
In $G *$ , every pair of vertices with a path between them in $G$ is now adjacent
The transitive closure provides reachability information about a digraph

The transitive closure can be computed by doing a DFS starting at each vertex. However, this takes $O (n (n + m))$ time. Alternatively, there is the Floyd-Warshall algorithm:

For the graph $G$ , number the vertices $1, 2, ..., n$
Compute the graphs $G_{0}, ..., G_{n}$
- $G_{0} = G$
- $G_{k}$ has directed edge $(v_{i}, v_{j})$ if $G$ has a directed path from $v_{i}$ to $v_{j}$ with intermediate vertices $v_{1}, ..., v_{k}$
Digraph $G_{k}$ is computed from $G_{k - 1}$
$G_{n} = G *$
Add $(v_{i}, v_{j})$ if edges $(v_{i}, v_{k})$ and $(v_{k}, v_{j})$ appear in $G_{k - 1}$

In pseudocode:

for k=1 to n
    Gk = Gk_1
      for i=1 to n (i != k)
          for j=1 to n (j != i, j!=k)
              if G_(k-1).areAdjacent(vi,vk) && G_(k-1).areAdjacent(vk,vj)
                  if !G_(k-1).areAdjacent(vi,vj)
                      G_k.insertDirectedEdge(vi,vj,k)
  return G_n

This algorithm takes $O (n^{3})$ time. Basically, at each iteration a new vertex is introduced, and each vertex is checked to see if a path exists through the newly added vertex. If it does, a directed edge is inserted to transitively close the graph.

Topological Ordering

A Directed Acyclic Graph (DAG) is digraph that has no directed cycles
A topological ordering of a digraph is a numbering $v_{1}, v_{2}, ..., v_{n}$ of the vertices such that for every edge $(v_{i}, v_{j})$ , $i < j$
- The vertex it points to is always greater than it
A digraph can have a topological ordering if and only if it is a DAG

A topological ordering can be calculated using a DFS:

public static void topDFS(Graph G, Vertex v){
    v.visited = true
    for(Edge e: v.edges){
        w = opposite(v,e)
        if(w.visited = false)
            topDFS(G,w)
        else{
            v.label = n
            n = n-1
        }
    }
}

The first node encountered in the DFS is assigned $n$ , the one after that $n - 1$ , and so on until all nodes are labelled.

Computer Systems Engineering Notes