Heaps

• A heap is a tree-based data structure where the tree is a complete binary tree
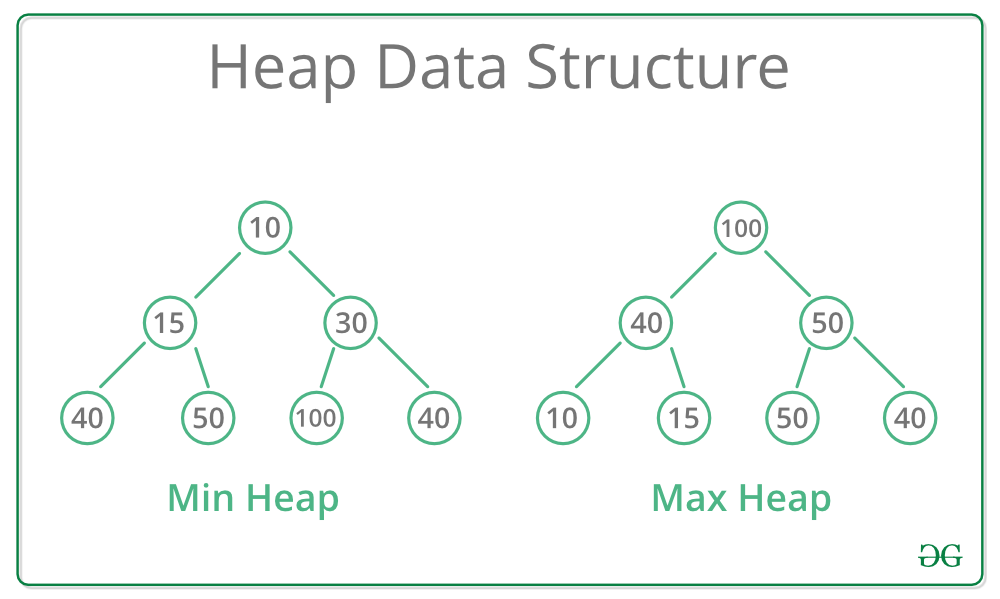
• Two kinds of heaps, min-heaps and max-heaps
• For a min-heap, the heap order specifies that for every internal node $v$ other than the root, $v\ge parent(v)$
  • In other words, the root of the tree/subtree must be the smallest node
  • This property is inverted for max heaps
• Complete binary tree means that every level of the tree, except possibly the last, is filled, and all nodes are as far left as possible.
  • More formally, for a heap of height $h$, for $i=0,1,...,h-1$ there are $2^i$ nodes of depth $i$
  • At depth $h-1$, the internal nodes are to the left of the external nodes
  • The last node of a heap is the rightmost node of maximum depth
• Unlike binary search trees, heaps can contain duplicates
• Heaps are also unordered data structures
• Heaps can be used to implement priority queues
  • An Entry(Key,Value) is stored at each node

Insertion

• To insert a node z into a heap, you insert the node after the last node, making z the new last node
  • The last node of a heap is the rightmost node of max depth
• The heap property is then restored using the upheap algorithm
• The just inserted node is filtered up the heap to restore the ordering
• Moving up the branches starting from the z
  • While parent(z) > (z)
    • Swap z and parent(z)
• Since a heap has height $\log n$, this runs in $O(\log n)$ time

Removal

• To remove a node z from the heap, replace the root node with the last node w
• Remove the last node w
• Restore the heap order using downheap
• Filter the replacement node back down the tree
  • While w is greater than either of its children
    • Swap w with the smallest of its children
• Also runs in $O(\log n)$ time

Heap Sort

For a sequence S of n elements with a total order relation on them, they can be ordered using a heap.

• Insert all the elements into the heap
• Remove them all from the heap again, they should come out in order
• $n$ calls of insert take $O(n\log n)$ time
• $n$ calls to remove take $O(n\log n)$ time
• Overall runtime is $O(n\log n)$
• Much faster than quadratic sorting algorithms such as insertion and selection sort

Array-based Implementation

For a heap with n elements, the element at position p is stored at cell f(p) such that

• If p is the root, f(p) = 0
• If p is the left child q, f(p) = 2*f(q)+1
• If p is the right child q, f(p) = 2*f(q)+2

Insert corresponds to inserting at the first free cell, and remove corresponds to removing from cell 0

• A heap with n keys has length $O(n)$