Lexing

We want to transform a stream of characters into a stream of tokens (token name, attribute value)

• A lexeme is the sequence of chars from source code
• A Regex is formal notation for a recogniser
• Recognisers are represented as finite automata
  • $S$ - finite set of states in the recogniser along with error state $S_e$
  • $\Sigma$ is finite alphabet used by recogniser
  • $\delta (s,c)$ is transition function
    • Maps states $s$ and characters $c$ to next state
  • $s_0$ is the start state
  • Set $S_A$ are accepting states
• An alphabet is a finite set of symbols
  • String is sequence of symbols from alphabet
  • Language is set of strings over the alphabet
    • Defined using grammars
  • We want to check if string on alphabet is a member of language
    • Use a recognising automaton
      • Diagrams are large, use regex to express
  • A language defined by a regex is the set of all strings that can be described by that regex

Tokenising

• Construct a regex matching all lexemes for all tokens
  • Union of regexes for the token classes gives a regex $R$ that defines a language
• Given an input sequence of characters, want to check if some number of characters belong to the language $R$
  • Gor $1\le i\le n$ check if $C_1,...,C_i$ is in $L(R)$
  • If true then we remove that string as a token and continue
  • Always select the longer sequence - maximal munch
  • If more than one token matches use the token class specified first
  • If no match then error
• Can build a scanner from regex
  • Require simulation of a DFA
  • Thompson’s construction goes from NFA -> RE
  • Subset construction builds a DFA that simulates an NFA
  • Hopcroft’s algorithm minimises a DFA
  • Kleene’s contruction dervices an RE from a DFA
• NFAs allow transitions on the empty string
  • States may have multiple transitions on the same character.
  • Can combine multiple FAs by just joining them with epsilon transisions
• DFAs only have a single transition on the each character from each state
  • No epsilon transitions
  • Can simulate any NFA

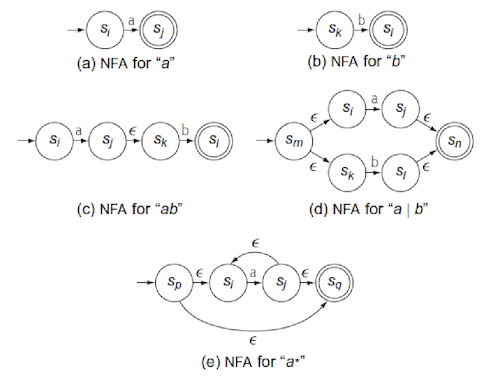
Thompson's Construction - RE to NFA

• Use a template for building an NFA that corresponds to
  • A single letter regex
  • Transformation on NFAs that models the effect of regex operators
  • Combine fragments using epsilon transitions
  • Take into account precedence

Subset Construction - NFA to DFA

Convert NFA to DFA to make it easier to simulate.

• Combine states based on epsilon transitions to eliminate them
• Create subset of states, then only consider transitions between subsets
• Set of states that can be reached from some state $n$ along only epsilon transitions is the epsilon closure of $n$

Where there are several possible choices of next state, take all choices simultaneously and form a set of the possible next states. This set of NFA states becomes a single DFA state.

Hopcroft's algorithm - Minimising a DFA

Some states can be merged - partition states into groups of states that produce the same behaviour on any input string.

• Start by partitioning into accepting and non-accepting states
• Consider each subgroup
  • Partition into new subgroups such that two states $s$ and $t$ are in the same subgroup iff for all input symbols $a$, $s$ and $t$ have transitons on $a$ into the same group $G$
  • Replace group with new partitioning
• Keep going until convergence