Translational Mechanical Systems

• Translational systems involve movement in 1 dimension
• For example, a the suspension in a car going over bumps going up and down
• System diagrams can be used to represent systems

• Diagrams include:
  • Masses
  • Springs
  • Dampers

Elements

There are element laws to model each of the three elements involved in mechanical systems. They are modelled using two key variables:

• Force $F(t)$ in newtons ($N$)
• Displacement $x(t)$ in meters ($m$)
  • Also sometimes velocity $v(t)=\dot{x}$ in meters per second ($m{s}^{-1}$)

When modelling systems, some assumptions are made:

• Masses are all perfectly rigid
• Springs and dampers have zero mass
• All behaviour is assumed to be linear

Mass

• Stores kinetic/potential energy
• Energy storage is reversible
  • Can put energy in OR take it out

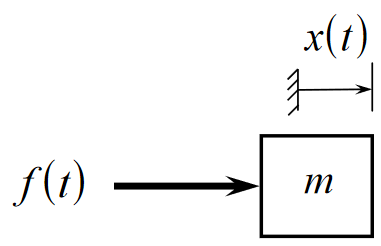
Elemental equation (Newton's second law):

$$m\frac{d^2}{d{t}^2}x=m\ddot{x}=ma=f(t)$$

Kinetic energy stored:

$$W=\frac{1}{2}m{v}^2$$

Spring

• Stores potential energy
• Also reversible energy store
  • Can be stretched/compressed

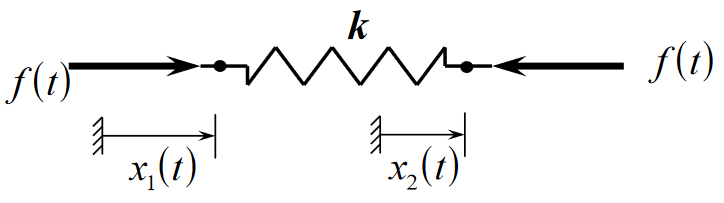
Elemental equation (Hooke's law):

$$f(t)=k(x_1(t)-x_2(t))$$

The spring constant k has units $N{m}^{-1}$. Energy Stored:

$$W=\frac{1}{2}k(x_1-x_2)$$

In reality, springs are not perfectly linear as per hooke's law, so approximations are made. Any mechanical element that undergoes a change in shape can be described as a stiffness element, and therefore modelled as a spring.

Damper

Dampers are used to reduce oscillation and introduce friction into a system.

• Dissapates energy as heat
• Non reversible energy transfer
• Takes energy out of the system

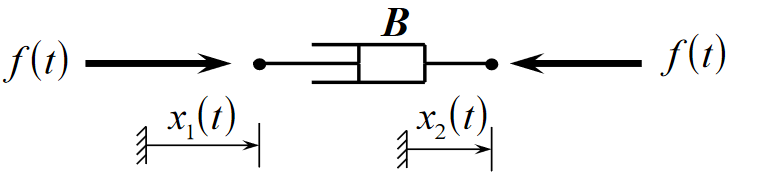
Elemental equation:

$$f(t)=B(\dot{x_1}-\dot{x_2})$$

B is the damper constant and has units $Ns{m}^{-1}$

Interconnection Laws

Compatibility Law

• Elemental velocities are identical at points of connection

Equilibrium Law

• Sum of external forces acting on a body equals mass x acceleration
• All forces acting on a body in equilibrium equals zero

Fictitious/D'alembert Forces

D'alembert principle is an alternative form of Newtons' second law, stating that the force on a body is equal to mass times acceleration: $F-ma=0$. $-ma$ is the inertial, or fictitious force. When modelling systems, the inertial force always opposes the direction of motion.

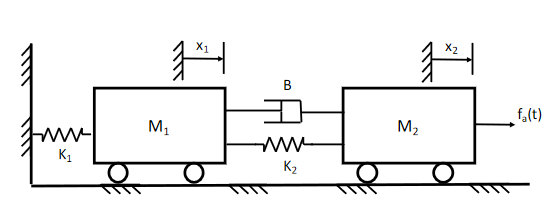
Example:

Form a differential equation describing the system shown below.

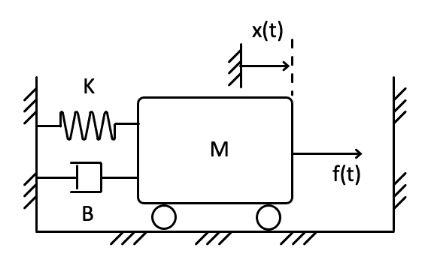
4 forces acting on the mass:

• Spring: $F=kx$
• Damper: $F=B\dot{x}$
• Inertial/Fictitious force: $F=m\ddot{x}$
• The force being applied, $f(t)$

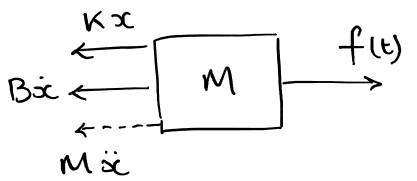
The forces all sum to zero:

$$f(t)-kx-B\dot{x}-m\ddot{x}=0$$ $$f(t)=m\ddot{x}+B\dot{x}+kx$$