Rotational Mechanical Systems

Dynamic Systems

• A system is a set of interconnected elements which transfer energy between them
• In a dynamic system, energy between elements varies with time
• Systems interact with their environments through:
  • Input
    • System depends on
    • Do no affect environment
  • Output
    • System does not depend on
    • Affects Environment
• Mathematical models of dynamic systems are used to describe and predict behaviour
• Models are all, always approximations

Lumped vs Distributed Systems

• In a lumped system, properties are concentrated at 1 or 2 points in an element
  • For example
    • Inelastic mass, force acts at centre of gravity
    • Massless spring, forces act at either end
  • Modelled as an ODE
  • Time is only independent variable
• In a distributed system, properties vary throughout an element
  • For example, non-uniform mass
  • Time and position are both independent variables
  • Can be broken down into multiple lumped systems

Linear vs Non-Linear Systems

• For non-linear systems, model is a non-linear differential equation
• For linear systems, equation is linear
• In a linear system, the resultant response of the system caused by two or more input signals is the sum of the responses which would have been caused by each input individually
  • This is not true in non-linear systems

Discrete vs Continuous Models

• In discrete time systems, model is a difference equation
  • output happens at discrete time steps
• In continuous systems, model is a differential equation
  • output is a continuous function of the input

Rotational Systems

Rotational systems are modelled using two basic variables:

• Torque $\tau$ measured in $Nm$
  • A twisting force
  • Analogous to force in Newtons
• Angular displacement $\theta$ measured in radians
  • Angular velocity $\omega =\dot{\theta }$
  • Analogous to displacement in meters

Element Laws

Moment of Inertia

• Rotational mass about an axis
• Stores kinetic energy in a reversible form
• Shown as rotating disc with inertia $J$, units $Kg{m}^2$

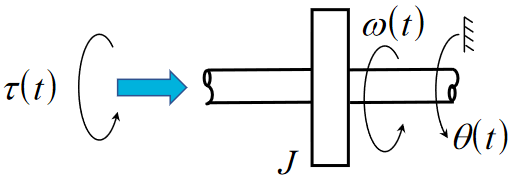
Elemental equation: $$\tau (t)=J\frac{d^2}{d{t}^2}\theta (t)=J\ddot{\theta }(t)$$

Energy Stored: $$W=\frac{1}{2}J{\omega }^2$$

The force $J\ddot{\theta }$ acts in the opposite direction to the direction the mass is spinning

Rotational Spring

• Stores potential energy by twisting
• Reversible energy store
• Produced torque proportional to the angular displacement at either end of spring

Elemental Equation:

$$\tau (t)=k({\theta }_1(t)-{\theta }_2(t))$$

Stored Energy:

$$W=\frac{1}{2}k({\theta }_1(t)-{\theta }_2(t){)}^2$$

Rotational Damper

• Dissapates energy as heat
• Non-reversible
• Energy dissapated $\propto$ angular velocity

Elemental Equation:

$$\tau (t)=B({\omega }_1(t)-{\omega }_2(t))$$

Interconnection Laws

Compatibility Law

Connected elements have the same rotational displacement and velocity

Interconnection Law

D'alembert law for rotational systems:

$$\sum _i({\tau }_{ext}{)}_i-J\dot{\omega }=0$$

$J\dot{\omega }$ is considered an inertial/fictitious torque, so for a body in equilibrium, ${\sum }_i{\tau }_i=0$.

Example

Form an equation to model the system shown below.

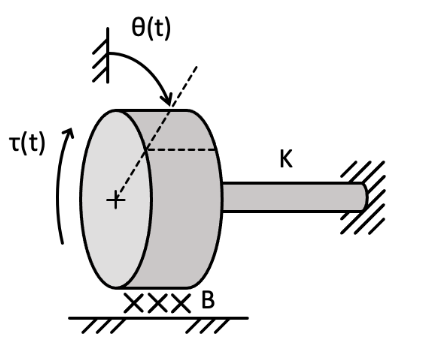
4 torques acting upon the disk:

• Stiffness element, $\tau =k\theta$
• Friction element, $\tau =B\dot{\theta }$
• Input torque $\tau (t)$
• Inertial force $\tau =J\ddot{\theta }$

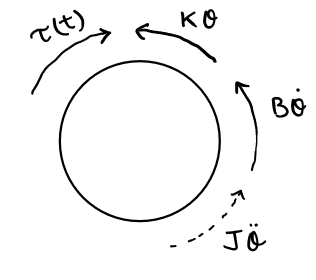
The forces sum to zero, so:

$$\tau (t)-k\theta -B\dot{\theta }-J\ddot{\theta }=0$$

$$\tau (t)=J\ddot{\theta }(t)+B\dot{\theta }(t)+k\theta (t)$$