Transfer Functions

• A transfer function is a representation of the system which maps from input to output
  • Useful for system analysis
  • Carried out in the Laplace Domain

The Laplace Domain

• Problems can be easier to solve in the Laplace domain, so the equation is Laplace transformed to make it easier to work with
• Given a problem such as "what is the output $y(t)$ given a differential equation in $y$ and the step input $u(t)$?"
  • Express step input in Laplace domain $U(s)$
  • Express differential equation in Laplace domain and find transfer function $G(s)$
  • Find output $Y(s)=U(s)G(s)$ in Laplace domain
  • Transfer back to time domain to get $y(t)$

The laplace domain is particularly useful in this case, as a differential equation in the time domain becomes an algebraic one in the Laplace domain. $$\mathcal{L}(\frac{dy}{dx})=sY(s)-y(0)$$

Transfer Function Definition

The transfer function is the ratio of output to input, given zero initial conditions. $$G(s)=\frac{Y(s)}{U(s)}$$

For a general first order system of the form $$T\frac{d}{dt}y(t)+y(t)=u(t)$$

The transfer function in the Laplace domain can be derived as: $$T\cdot \mathcal{L}(\frac{d}{dt}y(t))+\mathcal{L}(y(t))=\mathcal{L}(u(t))$$ $$T(sY(s))+Y(s)=U(s)$$ $$Y(s)(Ts+1)=U(s)$$ $$G(s)=\frac{Y(s)}{U(s)}=\frac{1}{Ts+1}$$

Step Input in the Laplace Domain

Step input has a constant value $H$ for $t>0$ $$\mathcal{L}(H)=\frac{H}{s}=U(s)$$

For a first order system, the output will therefore be: $$Y(s)=U(s)G(s)=\frac{H}{s}\frac{1}{Ts+1}$$ $$y(t)={\mathcal{L}}^{-1}(\frac{H}{s}\cdot \frac{1}{Ts+1})=H(1-e^{\frac{t}{T}})$$

Example

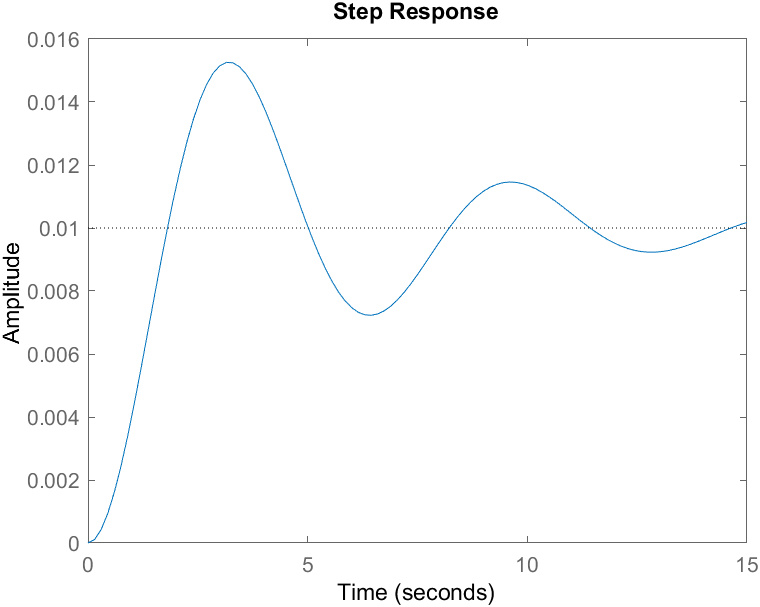
Find the transfer function for the system shown:

The system has input-output equation (in standard form): $$\frac{J}{B}\dot{\omega }(t)+\omega (t)=\frac{1}{B}\tau (t)$$

Taking the Laplace transform of both sides: $$\frac{J}{B}s\Omega (s)+\Omega (s)=\frac{1}{B}\mathrm{T}(s)$$

Rearranging to obtain the transfer function: $$G(s)=\frac{\Omega (s)}{\mathrm{T}(s)}=\frac{1}{B}\cdot \frac{1}{\frac{J}{B}s+1}=\frac{1}{Js+B}$$

Using Matlab

In matlab the tf function (Matlab docs) can be used to generate a system model using it's transfer function. For example, those code below generates a transfer function $G(s)=\frac{1}{2s+3}$, and then plots it's response to a step input of amplitude 1.

G = tf([1],[2 3]);
step(G);

Example

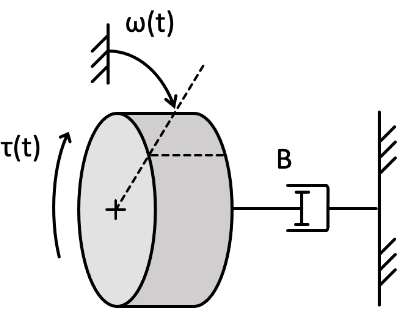
For the system shown below, where $M=100$, $B=40$, $K=100$, plot the step response and obtain the undamped natural frequency ${\omega }_n$ and damping factor $\zeta$.

$$G(s)=\frac{1}{s^{2}M+sB+K}=\frac{1}{100s^2+40s+100}$$

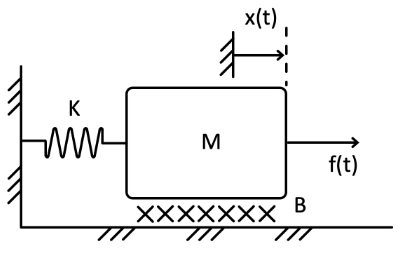
system = tf([1],[100 40 100]);
step(system, 15); % plot 15 seconds of the response

%function to obtain system parameters
[wn,z] = damp(system)

The script will output wn=1, and z = 0.2. The plotted step response will look like: