Bipolar Junction Transistors

There are two kinds of BJTs, NPN and PNP. Both have a base, collector, and emitter and consist of two PN-junctions.

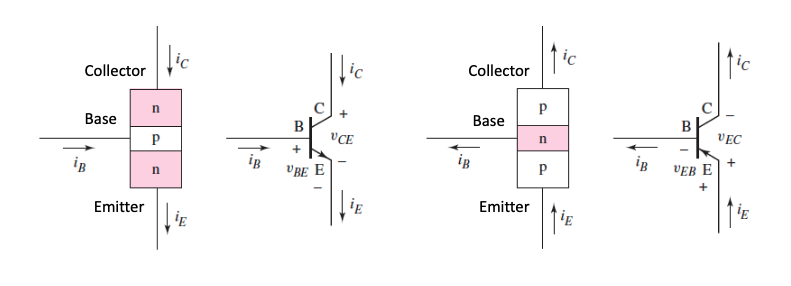
The operating mode of a BJT depends on how the junctions are biased.

• Forward active mode is used for amplification
• Cutoff and saturation modes are used for switching in digital circuits
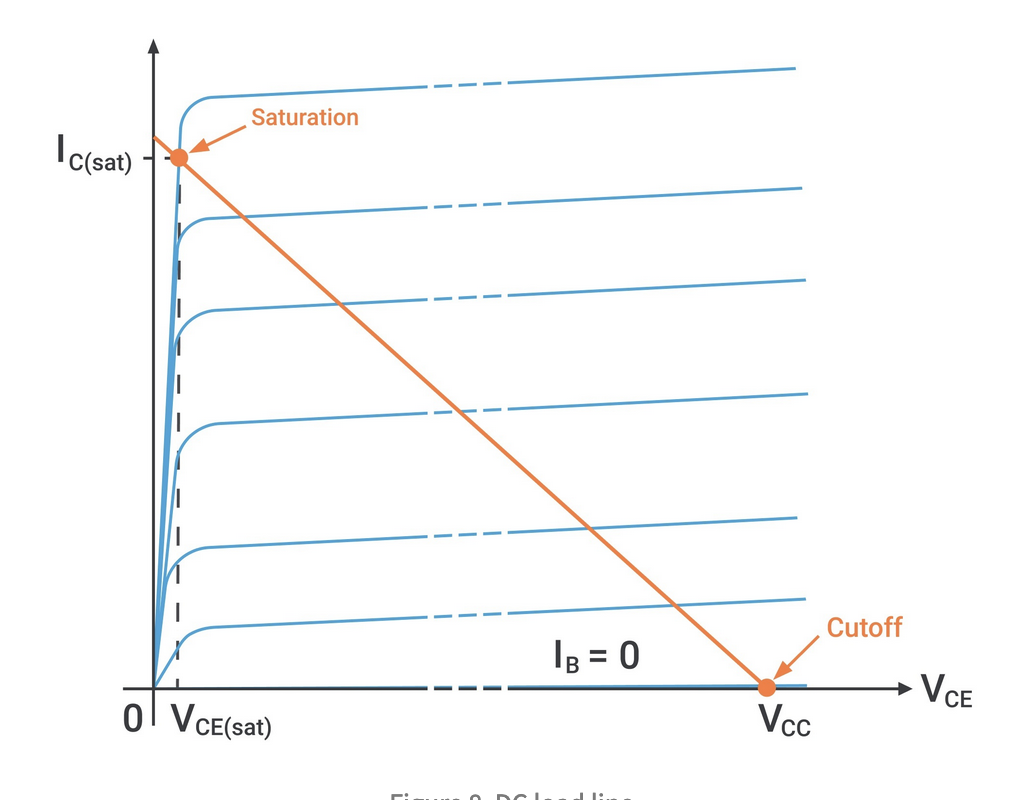
  • Cutoff is when both junctions are fully off
  • Saturation is when both junctions are fully on

Transistors obey KCL, so all currents entering a transistor must leave:

$$i_E=i_B+i_C$$

Transistors also have common-emitter current gain, $\beta$

$$i_C=\beta i_B$$

There is also the parameter $\alpha$, the common-base current gain:

$$\alpha =\frac{\beta }{1+\beta }{i}_E=\frac{i_C}{\alpha }$$

$\beta$ is usually large, so $\alpha \approx 1$

Large-Signal Model

BJTs operating in forward-active mode can be modelled as shown:

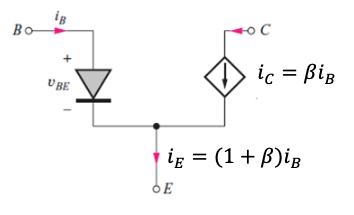
The current source shown is dependant upon the base current, and a diode is included to model the 0.7v drop across the PN-junction. This model assumes the transistor is biased correctly, as shown:

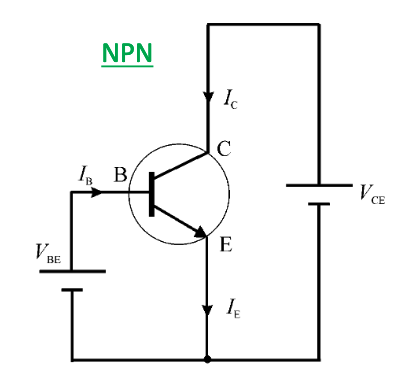
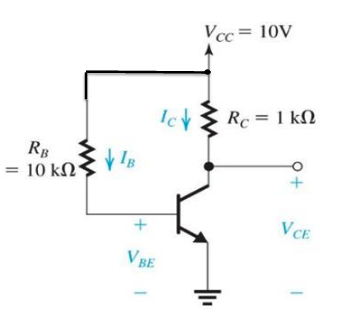
Biasing

Biasing is used to set up quiescent collector current to achieve optimum AC and DC conditions at the same time. $\beta$ is not well specified and can vary per device, so it should be designed to produce the correct operating conditions independent of device parameters and temperature. The Q-point is defined by $V_{CEQ}$ and $I_{C}Q$.

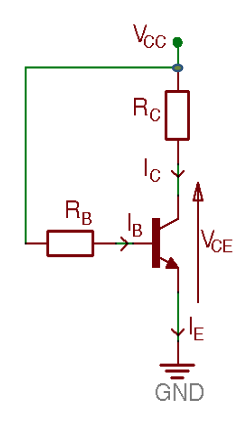
The circuit shows a single resistor base-biased circuit. Doing KVL around the base-emitter loop gives $I_{C}Q$:

$$V_{CC}=I_B{R}_B+V_{BE}$$

$$I_B=\frac{V_{CC}-V_{BE}}{R_B}$$

$$I_{CQ}=\beta I_B=\beta \frac{V_{CC}-V_{BE}}{R_B}$$

KVL between $V_{CC}$ and ground gives $V_{CEQ}$:

$$V_{CC}=I_C{R}_C+V_{CE}$$

$$V_{CE}=V_{CC}-I_C{R}_C$$

$$V_{CEQ}=V_{CC}-\beta \frac{V_{CC}-V_{BE}}{R_B}{R}_C$$

Equations depending on $\beta$ are bad though, because $\beta$ can vary too much to rely on it as a parameter. The graph below shows the same circuit with the same resistors, as $\beta$ varies:

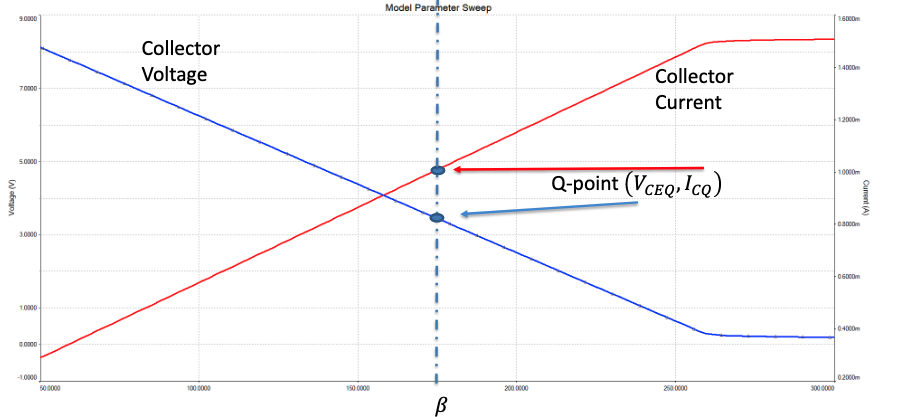
The Q-point shown is for $\beta =175$, which gives $V_{CEQ}=3.5V$ and $I_{CQ}=1mA$

Four-Resistor Voltage Divider Bias

This is the most widely used method to bias a BJT

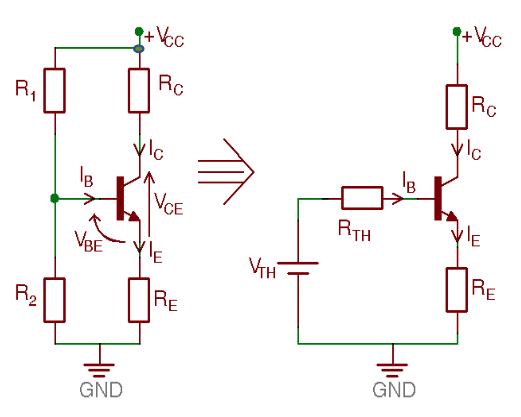
Thevenin's theorem is used to simplify the bias circuit

• $R_{TH}=R_1||R_2$
• $V_{TH}=V_C(R_2/(R_1+R_2))$

Applying KVL around the base-emitter loop:

$$V_{TH}=I_B{R}_{TH}+V_{BE}+I_E{R}_E$$

As $I_E=(1+\beta )I_B$:

$$V_{TH}=I_B{R}_{TH}+V_{BE}+(1+\beta )I_B{R}_E$$

$$I_B=\frac{V_{TH}-V_{BE}}{R_{TH}+(1+\beta )R_E}$$

Therefore, the collector current $I_C$:

$$I_C=\beta I_B=\beta \frac{V_{TH}-V_{BE}}{R_{TH}+(1+\beta )R_E}$$

Howere, we need to stabilise $I_C$ to not depend upon $\beta$. If we choose $R_{TH}$ to be small, ie $R_{TH}=\beta R_E/10$, then we can disregard it along with $\beta$:

$$I_C\approx \frac{\beta (V_{TH}-V_{BE})}{(1+\beta )R_E}\approx \frac{V_{TH}-V_{BE}}{R_E}\approx I_E$$

The equation (approximately) no longer depends upon $\beta$. Applying KVL around the collector-emitter loop for the voltage gives:

$$V_{CE}=V_{CC}-I_C{R}_C+R_E$$

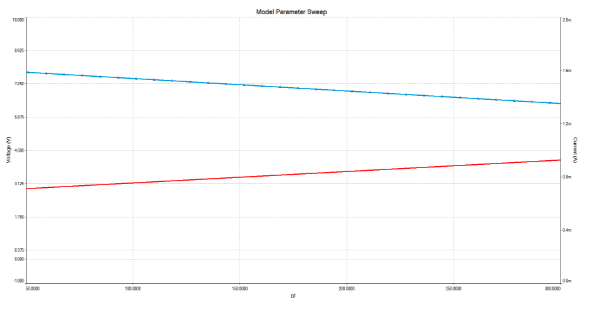
So, if $I_C$ is stable, then the Q-point $(V_{CEQ},I_{CQ})$ is bias-stable. Stability is achieved through the choice of a small enough, $R_{TH}$, and also the inclusion of an emitter resistor which provides negative feedback stabilisation.

Compare the graph below with the same one further up for the single-resistor bias circuit. The voltage/current are much more stable and less dependant up on $\beta$.

Transistors in Saturation

$$I_B=\frac{10-0.7}{10k}=0.93mA$$

$$I_C=\frac{50(1.7-0.7)}{10k}=45.6mA$$

$$V_C=10-46.5m\times 1k=-36.5V$$

This can't be correct. The model breaks down as the transistor is saturated, its no longer operating in the forward-active region.

• The voltage accross the collector/emitter maxes out at about 0.2v
• The transistor then turns on like a switch
• Collector to emitter is (roughly) a short circuit

When operating in saturation, $\beta$ becomes ${\beta }_{\text{forced}}$:

$${\beta }_{\text{forced}}=\frac{I_C}{I_B}=\frac{9.8}{0.93}=10.5$$

This is much lower than a typical $\beta$ would be. As $V_{BC}$ is increased further, $\beta$ decreases further and further.