Fourier Series and Transforms

Fourier Series

Fourier series provide a way of representing any periodic function as a sum of trigonometric functions. For a periodic function $f(t)$ with period $2L$, the Fourier series is given by:

$$f(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{a}_n\cos \frac{n\pi t}{L}+\sum _{n=1}^{\infty }{b}_n\sin \frac{n\pi t}{L}$$

Where the coefficients $a_n$ and $b_n$ are called the Fourier coefficients, integrals calculated over the period of the function:

$$a_0=\frac{1}{L}{\int }_{-L}^{L}f(t)dt{a}_n=\frac{1}{L}{\int }_{-L}^{L}f(t)\cos \frac{n\pi t}{L}dt{b}_n=\frac{1}{L}{\int }_{-L}^{L}f(t)\sin \frac{n\pi t}{L}dt$$

Note that if the function is even $f(t)=f(-t)$, then the $b_n$ term is always 0, and the series is comprised of cosine terms only:

$$f(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{a}_n\cos \frac{n\pi t}{L}$$

Likewise for odd functions $f(t)=-f(-t)$, the $a_n$ term is always zero, and the series is comprised of sine terms only:

$$f(t)=\sum _{n=1}^{\infty }{b}_n\sin \frac{n\pi t}{L}$$

The Fourier series uniquely represents a function if:

• The integral of function over its period is finite
• The function has a finite number of discontinuities over any finite interval
• Most (if not all) functions/signals of any engineering interest will satisfy these conditions

Exponential Representation

The Fourier series can be rewritten using Euler's formula $e^{j\theta }=\cos \theta +j\sin \theta$:

$$f(t)=\sum _{-\infty }^{\infty }{c}_n{e}^{j2n\pi t/T}$$

$$c_n=\frac{1}{T}{\int }_0^{T}f(t)e^{-j2n\pi t/T}dt\text{for}n=0,\pm 1,\pm 2,\pm \mathrm{3...}$$

Note that T = 2L, the period of the function.

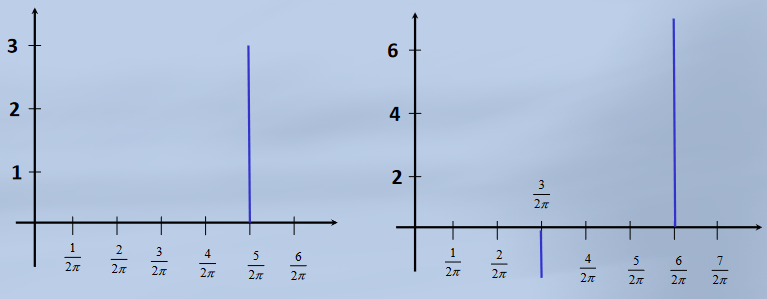
Frequency Spectrum Representation

The spectrum representation gives the magnitude $A_n$ and phase ${\varphi }_n$ of the harmonic components defined by the frequencies $f_n$ contained in a signal $f(t)$

$$f(t)=\sum _{n=1}^{\infty }{A}_n\sin (2\pi f_{n}t+{\varphi }_n)=\frac{a_0}{2}+\sum _{n=1}^{\infty }a\ast n\cos \frac{n\pi t}{L}+\sum ^{\infty }\ast n=1b_n\cos \frac{n\pi t}{L}$$

$$A_n=\sqrt{a_n^2+b_n^2}{\varphi }_n={\tan }^{-1}\frac{a_n}{b_n}{f}_n=\frac{n}{2L}$$

This gives two spectra:

• The frequency spectrum, describing the magnitude $A_n$ for each frequency $f_n$ present in the signal
• The phase spectrum, describing the phase ${\varphi }_n$ for each frequency $f_n$ present in the signal

The diagram below shows the frequency spectrum for the functions $f(t)=3\sin 5t$ and $f(t)=7\sin 6t-2\sin 3t$, respectively:

Example

Find the fourier series of the following function:

$$f(t)=\{\begin{array}{ll}-1& -\pi \le t\le 0\\ 1& 0\le t\le \pi \end{array}$$

$f(t)$ is an odd function with period $2\pi$ ($L=\pi$), hence we only need the $b_n$ integral:

$$b_n=\frac{1}{L}{\int }_{-L}^L\sin \frac{n\pi t}{L}dt=\frac{1}{\pi }\left({\int }_{-\pi }^0\sin nt+{\int }_0^{\pi }\sin nt\right)dt$$

$$=\frac{1}{\pi }\left(\left[\frac{1}{n}-\frac{1}{n}\cos (-\pi n)\right]+\left[-\frac{1}{n}\cos (n\pi )+\frac{1}{n}\right]\right)=\frac{2}{n\pi }\left(1-\cos (n\pi )\right)$$

Since $\cos n\pi =(-1{)}^n$:

$$b_n=\frac{2}{n\pi }(1-(-1{)}^n)$$

Can introduce a new index $k$, such that $n=2k-1$:

$$b_k=\frac{4}{2k\pi -\pi }\text{for}1,2,3,...,\infty$$

The Fourier series for $f(t)$ is therefore given by:

$$\frac{4}{\pi }\sum _{k=1}^{\infty }\frac{1}{2k-1}\sin \left((2k-1)t\right)$$

Fourier Transforms

Fourier series give a representation of periodic signals, but non periodic signals can not be analysed in the same way. The Fourier transform works by replacing a sum of discrete sinusoids with a continuous integral of sinusoids over frequency, transforming from the time domain to the frequency domain. A non-periodic function $f(t)$ can be expressed as:

$$f(t)={\int }_0^{\infty }A(\omega )\cos \omega t+B(\omega )\sin \omega td\omega$$

$$A(\omega )=\frac{1}{\pi }{\int }_{-\infty }^{\infty }f(t)\cos \omega tdtB(\omega )=\frac{1}{\pi }{\int }_{-\infty }^{\infty }f(t)\sin \omega tdt$$

Provided that:

• $f(t)$ and $f^{\prime }(t)$ are piecewise continuous in every finite interval
• ${\int }_{\infty }^{-\infty }|f(t)|dt$ exists

This can also be expressed in complex notation:

$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(\omega )e^{j\omega t}d\omega$$

$$F(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-j\omega t}dt$$

• $F(\omega )$ is the Fourier transform of $f(t)$, denoted $\mathcal{F}\{f(t)\}$
• $f(t)$ is the inverse Fourier transform of $F(\omega )$, denoted ${\mathcal{F}}^{-1}\{F(\omega )\}$

For periodic signals:

• Fourier series break a signal down into components with discrete frequencies
  • Amplitude and phase of components can be calculated from coefficients
  • Plots of amplitude and phase against frequency give frequency spectrum of a signal
  • The spectrum is discrete for periodic signals

For non-periodic signals:

• Fourier Transforms represent a signal as a continuous integral over a range of frequencies
  • The frequency spectrum of the signal is continuous rather than discrete
  • $|F(\omega )|$ gives the spectrum amplitude
  • $\arg (F(\omega ))$ gives the spectrum phase

Fourier Transform Properties

Fourier transforms have linearity, same as z and Laplace.

Time Shift

For any constant $a$:

$$\mathcal{F}\{f(t-a)\}=e^{-j\omega a}F(\omega )$$

If the original function $f(t)$ is shifted in time by a constant amount, this does not affect the magnitude of its frequency spectrum $F(\omega )$. Since the complex exponential always has a magnitude of 1, the time delay alters the phase of $F(\omega )$ but not its magnitude.

Frequency Shift

For any constant $a$:

$$\mathcal{F}\{e^{jat}f(t)\}=F(\omega -a)$$

Example

Find the Fourier integral representation of

$$f(t)=\{\begin{array}{ll}1& -1\le t\le 1\\ 0& |t|>1\end{array}$$

$$F(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-j\omega t}dt={\int }_{-1}^1(1)e^{-j\omega t}dt={\left[\frac{e^{-j\omega t}}{-j\omega }\right]}_{-1}^1$$

$$F(\omega )=\frac{e^{-j\omega }-e^{j\omega }}{j\omega }$$

This is the Fourier transform of $f(t)$. Using Euler's relation $\sin \theta =\frac{e^{j\theta }-e^{-j\theta }}{2j}$:

$$F(\omega )=\frac{e^{-j\omega }-e^{j\omega }}{j\omega }=\frac{2\sin \omega }{\omega }$$

Therefore, the integral representation is:

$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{2\sin \omega }{\omega }{e}^{j\omega t}d\omega$$