Broadband Matching

Multi-section transformers can be used where a wider bandwith of matching is required than can be achieved by a single $\lambda /4$ transformer.

Small Reflections

To derive such a transformer, we start with the theory of small reflections, applied to a single-section transformer. The incident wave will partially reflect and partially transmit at the $Z_1/Z_2$ interface, which will then reflect at the load, and then reflect again at the boundary, and so on.

$${\Gamma }_1=\frac{Z_2-Z_1}{Z_2+Z_1}{\Gamma }_2=-{\Gamma }_1{\Gamma }_3=\frac{Z_L-Z_2}{Z_L+Z_2}$$

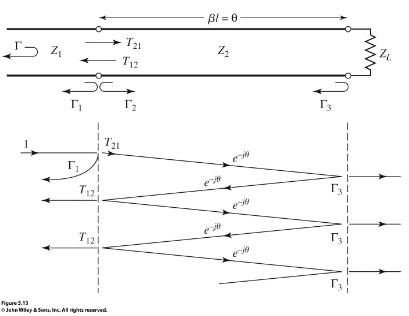
Summing the reflections/transmissions, the total reflection seen by the feedline is:

$$\Gamma ={\Gamma }_1+T_{12}{T}_{21}{\Gamma }_3{e}^{-2j\theta }\sum _{n=0}^{\infty }{\Gamma }_2^n{\Gamma }_3^n{e}^{-2jn\theta }$$

This is a geometric series, which sums to:

$$\Gamma =\frac{{\Gamma }_1+{\Gamma }_3{e}^{-2j\theta }}{1+{\Gamma }_1{\Gamma }_3{e}^{-2j\theta }}$$

Multisection Transformer

Consider now a multisection transformer, which is just lots of small sections of transmission line of equal length

$${\Gamma }_0=\frac{Z_1-Z_0}{Z_1+Z_0}{\Gamma }_n=\frac{Z_{n+1}-Z_n}{Z_{n+1}+Z_n}{\Gamma }_N=\frac{Z_L-Z_N}{Z_L+Z_N}$$

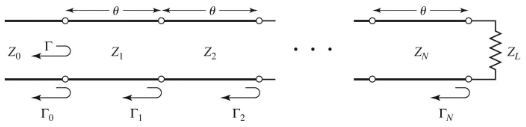
Making a few assumptions:

• Assume the differences between adjacent impedances are small
• Assume all $Z_n$ increase or decrease monotonically
• Assume $Z_L$ is real
  • ${\Gamma }_n$ will be real and of the same sign

The total reflection coefficient is therefore:

$$\Gamma (\theta )={\Gamma }_0+{\Gamma }_1{e}^{-2j\theta }+...+{\Gamma }_{N}e-2jN\theta$$

Any desired value of $\Gamma$ can be synthesised by suitably choosing ${\Gamma }_n$ and $N$.

The Binomial Transformer

We show how to realise such a transformer with a maximally flat total reflection coefficient, a binomial transformer.

For an $N$-section transformer:

• Set the first $N-1$ derivatives of $|\Gamma (\theta )|$ to 0 at the center frequency $f_0$
  • Provided by a reflection coefficient of the form $\Gamma (\theta )=A(1+e^{-2j\theta }{)}^N$
  • Magnitude is then $|\Gamma (\theta )|=2^N|A||\cos \theta {|}^N$
• To determine $A$, let $f\to 0$
  • $\theta =\beta \to 0$
  • Expression reduces to $\Gamma (0)=2^{N}A=\frac{Z_L-Z_0}{Z_L+Z_0}$
  • All sections are of 0 electrical length as $f\to 0$
  • $A=2^{-N}\frac{Z_L-Z_0}{Z_L+Z_0}$

$\Gamma (\theta )$ is expressed as a binomial series:

$$\Gamma (\theta )=A(1+e^{-2j\theta }{)}^N=A\sum _{n=0}^N{C}_n^N{e}^{-2jn\theta }{\Gamma }_n=A{C}_n^N$$

Because we assume ${\Gamma }_n$ are all small, we can approximate the characteristic impedances as:

$${\Gamma }_n=\frac{Z_{n+1}-Z_n}{Z_{n+1}+Z_n}\approx \frac{1}{2}\ln \frac{Z_{n+1}}{Z_n}$$

$$Z_{n+1}\approx \exp \left(\ln Z_n+2^{-N}{C}_n^N\ln \frac{Z_L}{Z_0}\right)$$

To find the bandwith of the binomial transformer, let ${\Gamma }_m$ be the maximum tolerated reflection coefficient over the passband.

$${\Gamma }_m=2^N|A|{\cos }^N{\theta }_m$$

${\theta }_m<\pi /2$ is the lower edge of the passband. Therefore:

$$\cos {\theta }_m=\frac{1}{2}{\left(\frac{{\Gamma }_m}{|A|}\right)}^{1/N}$$

And the fractional bandwith:

$$\frac{\Delta f}{f_0}=\frac{2(f_0-f_m)}{f_0}=2-\frac{4{\theta }_m}{\pi }$$