Network Parameters

Impedance & Admittance Parameters

• Consider an N-port microwave network
• Forward and backward voltage and current waves can be defined for TEM waves
  • Can define matrices of impedances(/admittances) to relate voltage and current port parameters to each other
• Ports may be any type of transmission line for a single propagating mode
• At a specified point on the $n_{th}$ port, a terminal place $t_n$ is defined
  • Terminal planes provide a phase reference for wave phasors
  • Equivalent incident and reflected voltage and current also defined

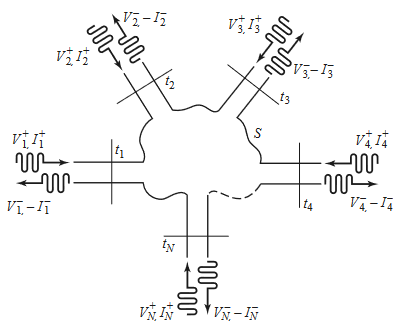
• At the $n_{th}$ terminal, total voltage and current are given by
  • $V_n=V_n^{+}+V_n^{-}$
  • $I_n=I_n^{+}+I_n^{-}$
  • Assumes coordinate along which propagation occurs is zero at terminal

The impedance matrix $V=ZI$ relates these voltages and currents:

$$\left[\begin{array}{c}{V}_1\\ V_2\\ ⋮\\ V_N\end{array}\right]=\left[\begin{array}{cccc}{Z}_{11}& Z_{12}& \dots & Z_{1N}\\ Z_{21}& Z_{22}& \dots & Z_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ Z_{N1}& Z_{N2}& \dots & Z_{NN}\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_2\\ ⋮\\ I_N\end{array}\right]$$

Can similarly define an admittance matrix $I=YV$

$$\left[\begin{array}{c}{I}_1\\ I_2\\ ⋮\\ I_N\end{array}\right]=\left[\begin{array}{cccc}{Y}_{11}& Y_{12}& \dots & Y_{1N}\\ Y_{21}& Y_{22}& \dots & Y_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ Y_{N1}& Y_{N2}& \dots & Y_{NN}\end{array}\right]\left[\begin{array}{c}{V}_1\\ V_2\\ ⋮\\ V_N\end{array}\right]$$

The two matrices are inverses of each other: $Y=Z^{-1}$. Both matrices relate total port voltages and currents.

$Z_{ij}$ can be found by driving port $j$ with current $I_j$, open circuiting all other ports, and measuring the open circuit voltage at port $i$

$$Z_{ij}=\frac{V_i}{I_j}{|}_{I_k=0\text{for}k\ne j}$$

$Z_{ii}$ is the input impedance looking into port $i$, and $Z_{ij}$ is the transfer impedance between ports $i$ and $j$.

The admittance matrix parameters are found similarly:

$$Y_{ij}=\frac{I_i}{V_j}{|}_{V_k=0\text{for}k\ne j}$$

• If a network is reciprocal (contains no active devices), then the matrix is symmetric
  • $Y_{ij}=Y_{ji}$
  • $Z_{ij}=Z_{ji}$
• For a reciprocal lossless network, all the $Z_{ij}$ or $Y_{ij}$ elements are purely imaginary
  • $Re(Z_{mn})=0$ for any $m$ and $n$

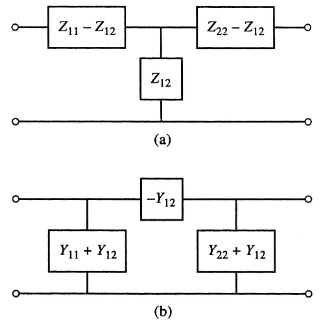
Any two port network can be reduced to an equivalent $T$ or $\Pi$ network:

Scattering Parameters

• Direct measurements of voltage and current become not that useful at high frequency because of waves
• The scattering matrix representation is more in line with the direct measurement of waves
• Provides a complete description of an $N$-port network, relating incident and reflected waves on ports.

The S-matrix is defined $V^{-}=S{V}^{+}$

$$\left[\begin{array}{c}{V}_1^{-}\\ V_2^{-}\\ ⋮\\ V_N^{-}\end{array}\right]=\left[\begin{array}{cccc}{S}_{11}& S_{12}& \dots & S_{1N}\\ S_{21}& S_{22}& \dots & S_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ S_{N1}& S_{N2}& \dots & S_{NN}\end{array}\right]\left[\begin{array}{c}{V}_1^{+}\\ V_2^{+}\\ ⋮\\ V_N^{+}\end{array}\right]$$

$S_{ij}$ is found by sending port $j$ an incident wave $V_j^{+}$ and measuring at port $i$ the reflected amplitude $V_i^{-}$. The incident waves on the rest of the ports are set to 0, meaning all ports are terminated in matched loads to avoid reflections.

$$S_{ij}=\frac{V_i^{-}}{V_j^{+}}{|}_{V_k^{+}=0\text{for}k\ne j}$$

• $S_{ii}$ is the reflection coefficient looking into port $i$
• $S_{ij}$ is the transmission coefficient (gain) from port $i$ to $j$
• The scattering matrix for a reciprocal network is symmetric $S=S^T$
• The scattering matrix fro a lossless network is unitary $S^T{S}^{\ast }=I$
  • Identity

Shifting Reference Planes

In the original network, the terminal planes are assumed to be at $z_n=0$, where $z_n$ is measured along the lossless line feeding the $n_{th}$ port. The matrix with this set of planes is $S$. If the new reference planes are defined $z_n=l_n$, then we get a new scattering matrix defined $V^{\prime -}=S^{\prime }{V}^{\prime +}$. From travelling waves on a lossless line:

$$V_n^{\prime +}=V_n^{+}{e}^{j{\beta }_n{l}_n}{V}_n^{\prime -}=V_n^{-}{e}^{j{\beta }_n{l}_n}$$

We can use this shift to define $S^{\prime }$ in terms of $S$

$$S^{\prime }=\left[\begin{array}{cccc}{e}^{-j{\beta }_1{l}_1}& 0& \dots & 0\\ 0& e^{-j{\beta }_2{l}_2}& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & e^{-j{\beta }_N{l}_N}\end{array}\right]S\left[\begin{array}{cccc}{e}^{-j{\beta }_1{l}_1}& 0& \dots & 0\\ 0& e^{-j{\beta }_2{l}_2}& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & e^{-j{\beta }_N{l}_N}\end{array}\right]$$

Transmission (ABCD) Parameters

Practical microwave networks consist of a cascade connection of two or more 2-port networks. It is useful to define a 2x2 transmission, or ABCD matrix, for each 2-port network such that the transmission matrix of the cascade connection can be obtained as the product of the transmission matrices of the individual networks.

$$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}{V}_2\\ I_2\end{array}\right]$$

Note the sign convention, which has $I_1$ flowing into port 1, and $I_2$ flowing out of port 2.

If two networks are cascaded, ie network 1 outputs into network 2, the transmission matrix of the cascaded network is the product of the two individually

$$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}{A}_1& B_1\\ C_1& D_1\end{array}\right]\left[\begin{array}{c}{V}_2\\ I_2\end{array}\right]\left[\begin{array}{c}{V}_2\\ I_2\end{array}\right]=\left[\begin{array}{cc}{A}_2& B_2\\ C_2& D_2\end{array}\right]\left[\begin{array}{c}{V}_3\\ I_3\end{array}\right]$$

$$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}{A}_1& B_1\\ C_1& D_1\end{array}\right]\left[\begin{array}{cc}{A}_2& B_2\\ C_2& D_2\end{array}\right]\left[\begin{array}{c}{V}_3\\ I_3\end{array}\right]$$

Some useful ABCD parameters for common networks are shown below

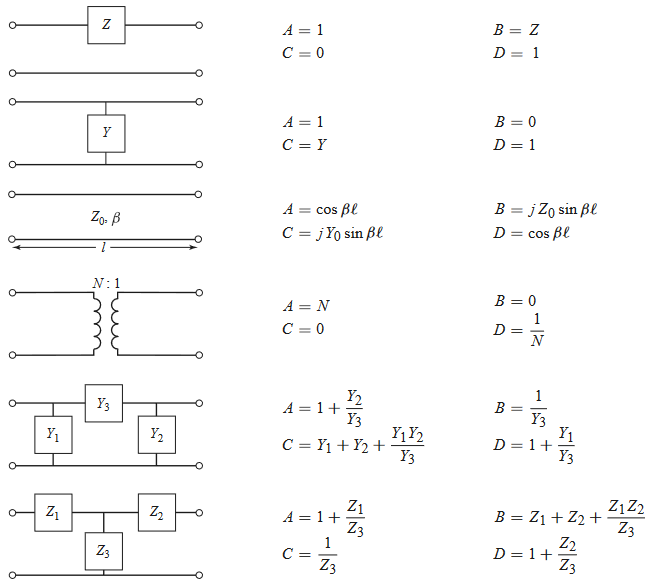
Port Parameter Conversion Table