Transmission Lines

A transmission line is a two port network that connects a source to a load

Modes

• Modes descibe the field pattern of propogating waves
  • Can be found by solving Maxwell's equations in a transmission line
• In a transmission line, electric and magnetic fields are orthogonal to each other, and both orthogonal to the direction of propogation
  • This is TEM (Transverse Electromagnetic) mode
• A TEM transmission line is represented by two parallel wires
  • To reason about voltages and currents within it, we divide it into differential sections $\delta z$
  • Each section is represented by an equivalent lumped element circuit

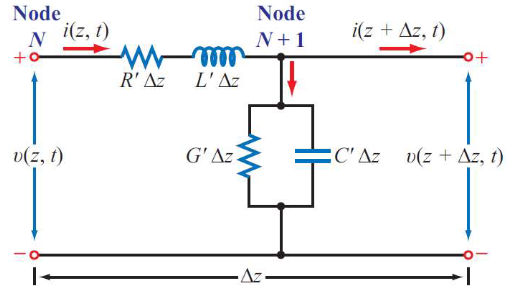
• $R^{\prime }$ - the combined resistance of both conductors per unit length, in $\Omega /m$
• $L^{\prime }$ - the combined inductance of both conductors per unit length, in $H/m$
• $C^{\prime }$ - the combined capacitance of both conductors per unit length, in $F/m$
• $G^{\prime }$ - the conductance of the insulation medium between the two conductors per unit length, in $S/m$

The table below gives parameters for some common transmission lines

• Conductors have magnetic permeability ${\mu }_c$ and conductivity ${\sigma }_c$
• The insulating/spacing material has permittivity $\epsilon$, permeability $\mu$ and conductivity ${\sigma }_c$
• All TEM transmission lines share the relations
  • $L^{\prime }{C}^{\prime }=\mu \epsilon$
  • $G^{\prime }/C^{\prime }=\sigma /\epsilon$
• The constant propogation constant of a line $\gamma =\alpha +j\beta =\sqrt{(R^{\prime }+j\omega L^{\prime })(G^{\prime }+j\omega C^{\prime })}$
  • $\alpha$ is the attenuation constant (Np/m)
  • $\beta$ is the phase constant (rad/m)
• The travelling wave solutions of a line are
  • $\tilde{V}(z)=V_0^{+}{e}^{-\gamma z}+V_0^{-}{e}^{\gamma z}$
  • $\tilde{I}(z)=I_0^{+}{e}^{-\gamma z}+I_0^{-}{e}^{\gamma z}$
  • $z$ represents position along th eline
  • $V_0^{+},I_0^{+}$ represents the incident wave from source to load
  • $V_0^{-},I_0^{-}$ represents the reflected wave from load to source

We therefore have the characterisitic impedance of the TEM transmission line:

$$Z_0=\frac{V_0^{+}}{I_0^{+}}=-\frac{V_0^{-}}{I_0^{-}}=\sqrt{\frac{R^{\prime }+j\omega L^{\prime }}{G^{\prime }+j\omega C^{\prime }}}$$

Both the voltage and current waves propagate with a phase velocity $u_p=f\lambda$. The presence of the two waves propagating in opposite directions produces a standing wave.

The Lossless Transmission Line

In most practical situations, we can assume a transmission line to be lossless:

• $R^{\prime }\ll \omega L^{\prime }$, and $G\ll \omega C^{\prime }$
• Assume $R^{\prime }=G^{\prime }\approx 0$, so $\gamma =j\omega \sqrt{L^{\prime }{C}^{\prime }}$
• Therefore, as $\gamma =\alpha +j\beta$:
  • $\alpha =0$
  • $\beta =\omega \sqrt{L^{\prime }{C}^{\prime }}=\omega \sqrt{\mu \epsilon }$
  • $Z_0=\sqrt{L^{\prime }/C^{\prime }}$

This then gives velocity and wavelength:

$$u_p=\frac{\omega }{\beta }=\frac{1}{\sqrt{L^{\prime }{C}^{\prime }}}=\frac{1}{\sqrt{\mu \epsilon }}\lambda =\frac{2\pi }{\beta }=\frac{2\pi }{\omega \sqrt{L^{\prime }{C}^{\prime }}}=\frac{1}{f\sqrt{\mu \epsilon }}$$

As the insulating material is usually non-magnetic, we have $\mu ={\mu }_0$

$$c=\frac{1}{\sqrt{{\mu }_0{\epsilon }_0}}{u}_p=\frac{c}{{\sqrt{\epsilon }}_r}\lambda =\frac{c}{f\sqrt{{\epsilon }_r}}=\frac{{\lambda }_0}{{\sqrt{\epsilon }}_r}$$

Voltage Reflection Coefficient

Assume a transmission line in which the signals are produced by a generator with impedance $Z_g$ and is terminated by a load impedance $Z_L$.

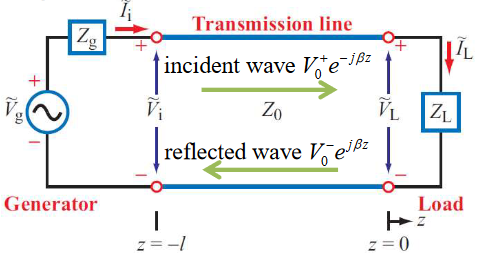
At any position on the line, the total voltage and current is:

$$V(z)=V_0^{+}{e}^{-\gamma z}+V_0^{-}{e}^{\gamma z}I(z)=\frac{V_0^{+}}{Z_0}{e}^{-\gamma z}+\frac{V_0^{-}}{Z_0}{e}^{\gamma z}$$

At the load at position $z=0$, the load impedance is:

$$Z_L=\frac{V_L}{I_L}$$

Using this we can find an expression for the ratio of backwards wave amplitude and forward wave amplitude. We obtain the equation below, the voltage reflection coefficient

$$\Gamma =\frac{V_0^{-}}{V_0^{+}}=\frac{Z_L-Z_0}{Z_L+Z_0}$$

• $Z_0$ for a lossless line is a real number, but $Z_L$ may be a complex quantity
• In general, the reflection coefficient is also complex, $\Gamma =|\gamma |\exp (j{\theta }_{\Gamma })$
  • Note that $|\Gamma |\le 1$, always
• A load is matched to a line when $Z_L=Z_0$, as then $\Gamma =0$
  • No reflection by the load $V_0^{-}=0$
• If $Z_L=\infty$ then $\Gamma =1$, then $V_0^{-}=V_0^{+}$
  • Open circuit load
• If $Z_L=0$ then $\Gamma =-1$, then $V_0^{-}=-V_0^{+}$
  • Short circuit load

Standing Waves

The standing wave equation gives an expression for the standing wave voltage at position $z=-l$

$$|\tilde{V}(z=-l)|=|V_0^{+}||(1+|\Gamma |e^{j({\theta }_{\Gamma }-2\beta l)})|$$

The ratio of $|V{|}_{max}$ to $|V{|}_{min}$ is called the Voltage Standing Wave Ratio, or VSWR. Max occurs when $e^{j({\theta }_{\Gamma }-2\beta l)}=1$, and min occurs when $e^{j({\theta }_{\Gamma }-2\beta l)}=-1$

Input Impedance of Lossless Lines

The input impedance $Z_{in}$ of a transmission line is the ratio of the total voltage to the total current at any point $z=-l$ on the line

$$Z_{in}=Z(z=-l)=\frac{V(z=-l)}{I(z=-l)}=Z_0\frac{1+\Gamma e^{-j2\beta l}}{1-\Gamma e^{-j2\beta l}}=Z_0\frac{Z_L+j{Z}_0\tan (\beta l)}{Z_0+j{Z}_L\tan (\beta l)}$$

• For a short circuit line $Z_L=0$, $Z_{in}=j{Z}_0\tan (\beta l)$
• For an open circuit line $Z_L=\infty$, $Z_{in}=-j{Z}_0\cot (\beta l)$