The Smith Chart

The Smith chart is a graphical tool for analysing and designing transmission line circuits. It represents the reflection coefficient's complex plane.

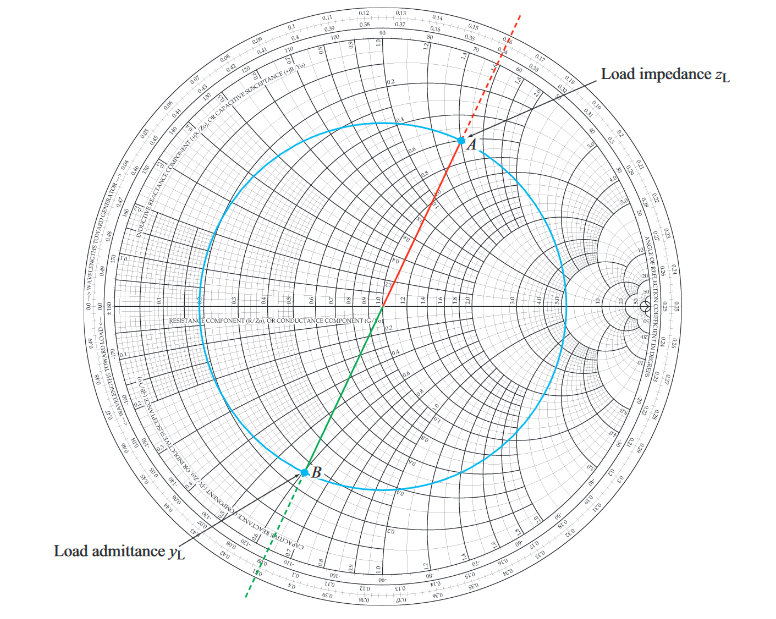
The image below shows the the complex plane

• Point A is the reflection coefficient $\Gamma =0.3+j0.4=0.5e^{j53^{\circ }}$
• Point B is the reflection coefficient $\Gamma =-0.5-j0.2=0.54e^{j202^{\circ }}$

The Smith chart shows circles of constant normalised resistance $r_L$, and constant normalised reactance $x_L$, within the unit circle plane.

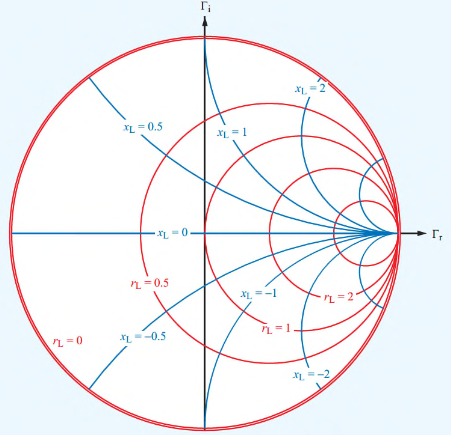
Given the normalised value of a load impedance $z_l=Z_L/Z_0=r_L+j{x}_L$, we can find the value of the corresponding reflection coefficient, and vice-versa.

Example

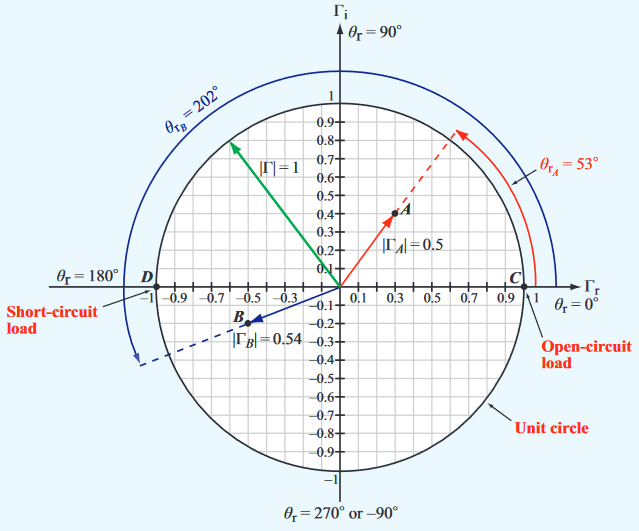
In the example below, point $P$ is plotted on the $r_L=2$ and $x_L=-1$ lines, representing a normalised impedance of $z_L=2-j$.

• The length of the line between the $P$ and the centre $O$ corresponds to the magnitude of the reflection coefficient
• The angle between the x axis and the point $P$ is $-26.6^{\circ }$
• $\Gamma =0.45e^{-j26.6}$

Phase Shifting

Based on the input impedance in terms of the reflection coefficient, we obtain

$$z(-l)=\frac{Z(z=-l)}{Z_0}=\frac{1+\Gamma e^{-j2\beta l}}{1-\Gamma e^{-j2\beta l}}=\frac{1+{\Gamma }_l}{1-{\Gamma }_l}$$

${\Gamma }_l$ is the phase shifted reflection coefficient. $\Gamma$ at $z=-l$ on a transmission line is equal to the reflection coefficient at the load ($z=0$), shifted by $-2\beta l$:

$${\Gamma }_l=\Gamma e^{-j2\beta l}=|\Gamma |e^{j{\theta }_{\Gamma }}{e}^{-j2\beta l}=|\Gamma |e^{j({\theta }_{\Gamma }-2\beta l)}$$

This phase shift can be achieved on the Smith chart by maintaining constant magnitude, and decreasing the phase ${\theta }_L$ by the phase, corresponding to a clockwise rotation of an angle $2\beta l$ radians.

A complete rotation of $2\pi$ radians corresponds to a change in length of $l=\lambda /2$. The outermost scale on the chart "wavelengths toward the generator" denotes movement on the transmission line toward the source, in units of wavelength.

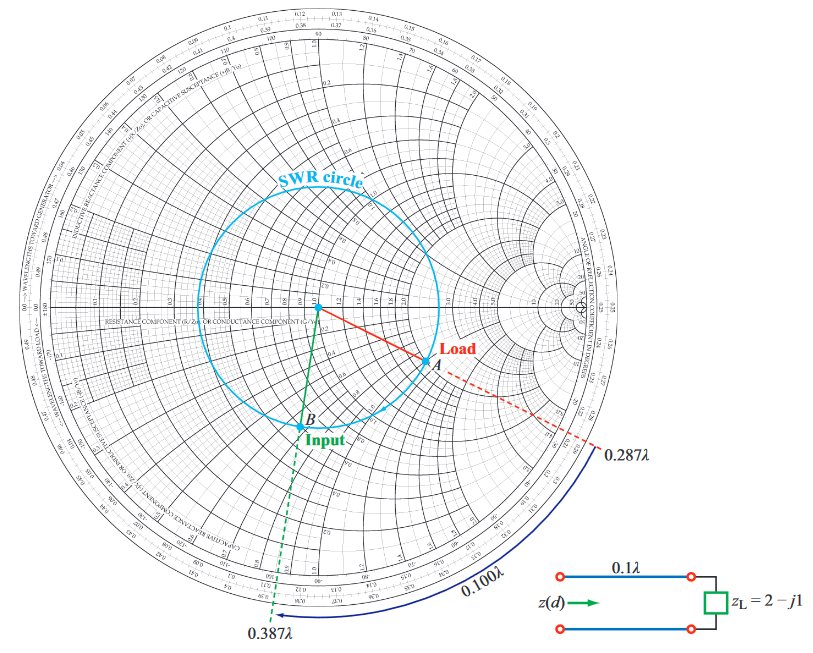
Example

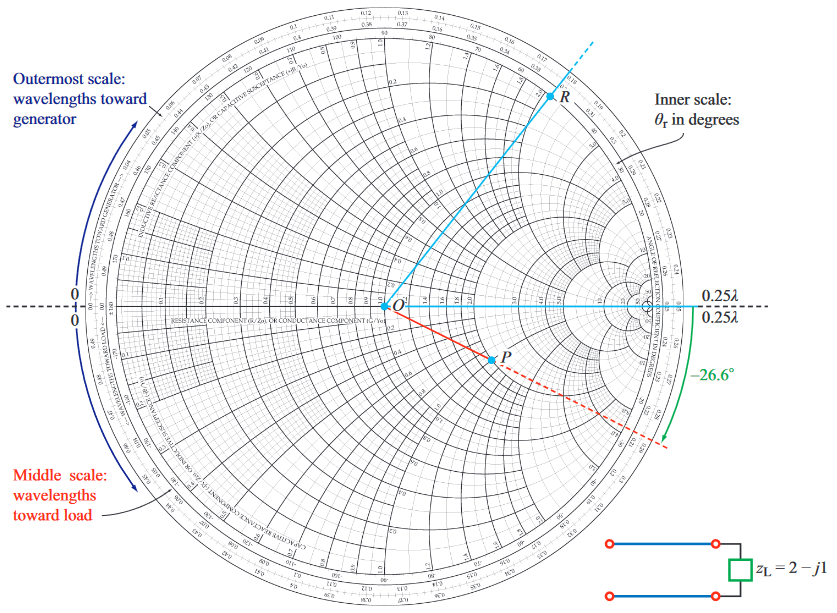
Point $A$ is a normalised load of $z_L=2-j$ at $0.287\lambda$. If the load terminates a transmission line of length $0.1\lambda$, what it's input impedance?

• Move clockwise by $0.1\lambda$ around a constant $|\Gamma |$ circle
• Read the smith chart at point $B$ to get $z_{in}=0.6-j0.66$

Admittance

For some problems, it is more convenient to work with admittances than with impedances

$$Y=G+jB=\frac{1}{Z}=\frac{1}{R+jX}$$

Normalised admittance $y$ is therefore:

$$y=\frac{Y}{Y_0}=\frac{G}{Y_0}+jB{Y}_0=g+jb$$

• Rotation by $\lambda /4$ on the SWR circle transforms $z$ into $y$, and vice-versa
• $r_L$ circles become $g_L$ circles
• $x_{L}circles$ become $b_L$ circles

Example

Point $A$ represents a normalised load impedance of $z_L=0.6+j1.4$. Moving on the SWR circle by $\lambda /4$ gives point $B$, the corresponding normalised admittance of $y_L=0.25-j0.6$